线段树区间更新操作

在之前的文章中，我们已经学习了如何使用线段树来做一些常规的区间操作：如何建树、单点更新、区间查询。这些操作通过线段树这种数据结构的特点，将单点更新和区间查询的复杂度都统一到 $$O(logn)$$ ，在海量查询场景下的开销也降低了很多。

那么关于线段树的讨论就到此为止了吗？其实并不是。我们学到的还只是冰山一角。这篇文章，我们来讨论一下如何通过线段树来实现区间更新。区间更新的操作在这里指的是对某一个范围的数进行增加或减少同一个常数的操作。例如数组 [2, 3, 4, 5, 6] ，对其下标 [0, 2] 进行区间更新都增加 10 ，则数组会变成 [12, 13, 14, 5, 6] 。

以下对于线段树的讨论全部以区间和场景为准。

单点更新遍历

当我们讨论区间更新的时候，肯定已经有读者开始思考：只要我们遍历一下区间的每一个值，执行单点更新不就可以了？

从结果上来看，这么做完全可以。从复杂度上来看，以 $$O(nlogn)$$ 复杂度执行一次长度为 $$n$$ 的区间更新。

我们回过头来看我们引出线段树目的是什么？为了实现常数复杂度时间构造和对数复杂度的操作。那么，我们有没有方式将区间更新操作通过对数复杂度 $$O(logn)$$ 时间来更新一个区间的数值呢？

考虑查询时候的行为

上文介绍的 query 操作总结成动图如下（假设我们有下标 [1, 8] 8 个元素构成的区间和线段树，此时我们要查询 [1, 6] 这个区间）：

区间查询

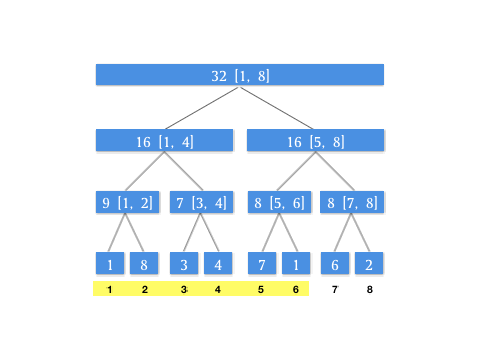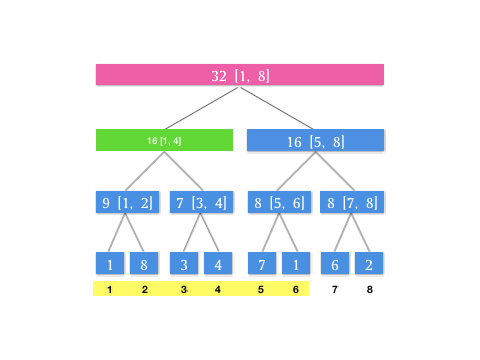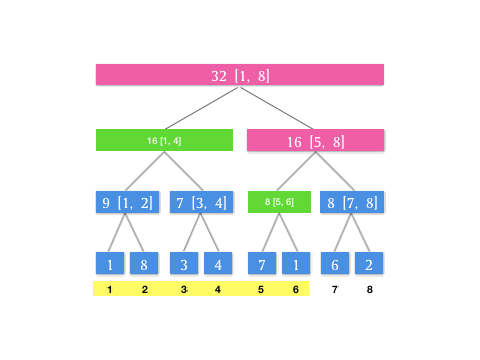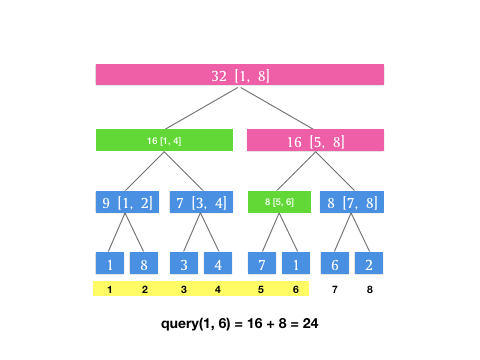
我们可以发现，其实在每次查询的时候，是不断对当前层级所表示的区间进行二分分治，直到最后每个分块的并集即为待查询区间。

另外线段树还有一个特点：由于我们引入的 push_up 操作，这就会让线段树有这么一个特点：父亲结点是包括子结点的状态。这是一个什么意思呢？拿区间和为例，push_up 是通过子结点数值求和来构造父结点，即：

tree[rt] = tree[rt * 2] + tree[rt * 2 + 1]

由于这个核心操作，我们发现我们描述的线段树是一种下级扩展上级的结构。当查询的时候，如果查询的节点所描述的区间符合要求，则会被计算到结果中。

要确定一个目标，我们的节点更新其实是为了查询到最新的结果。

所以有这么一个思路， 对所有查询范围中最小粒度的节点进行更新，从而就能让所有的查询操作返回最新的情况。什么是范围中最小粒度的节点呢？其实就是要满足两个特点：

在查询范围中；
尽量在线段树的上层。

增量记录

根据查询自上到下的特点，我们来维护一个增量数组，这个增量数组代表对应的节点待更新的增量。假设我们对上面动图上的线段树进行一个区间更新的操作，将 [3, 6] 这个区间上的所有数字增加 4 。此时我们的增量数组如图所示：

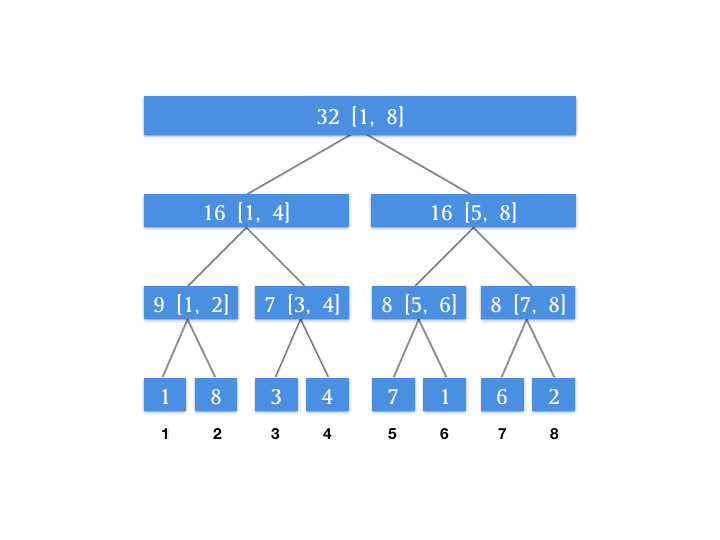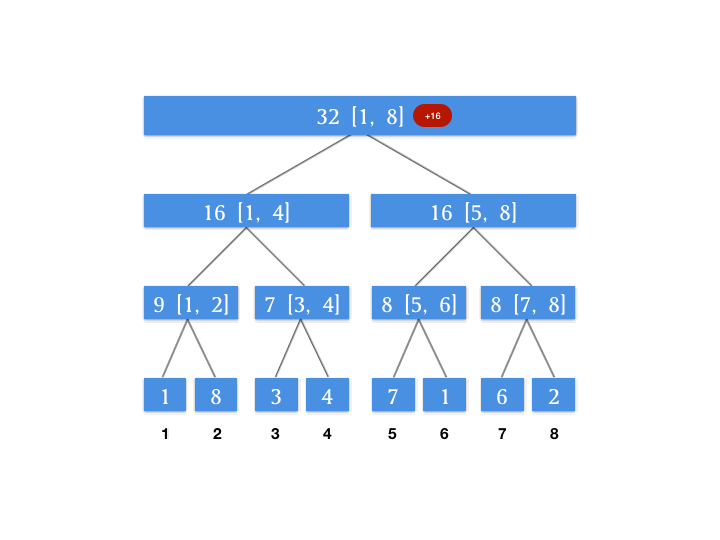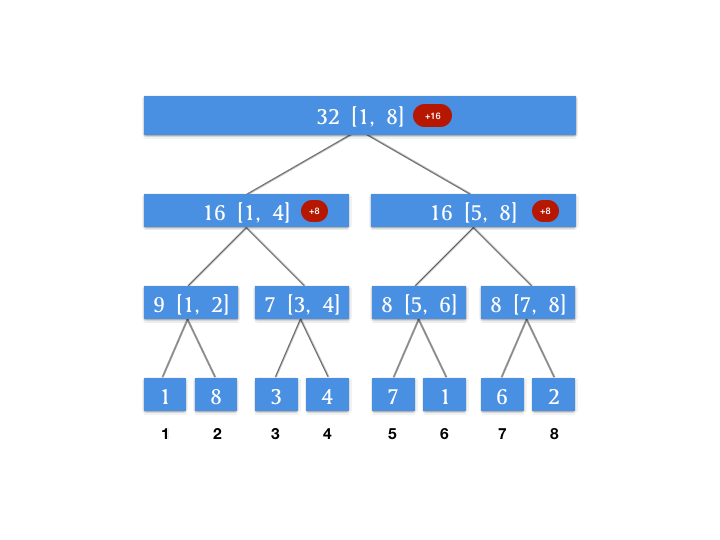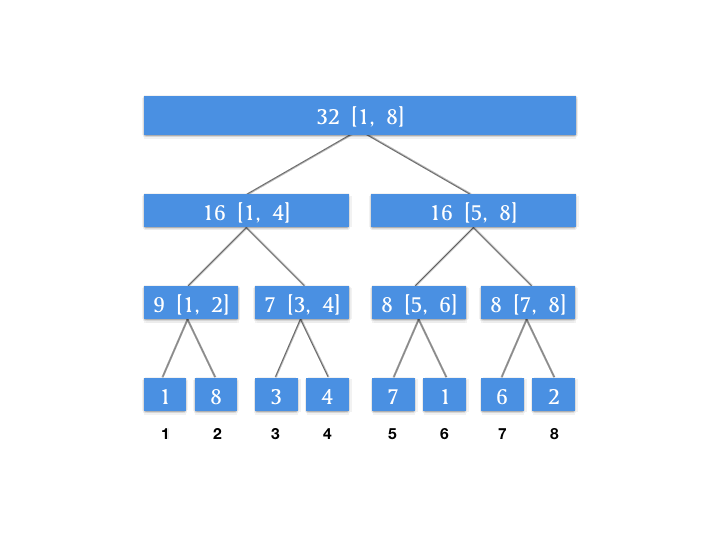
为什么要单独用一个属性来记录增量？因为我们上面的图片发现我们需要查的 [1, 6] 这个区间，其最小颗粒度的查询节点是 [1, 4] 和 [5, 6] 这两个节点，所以我们将增量向下更新到这两个节点，就能保证我们查询 [1, 6] 这个区间的正确性。

于是，通过这个思路我们来思考，当我们需要对一个区间进行批量增减操作的时候，我们只要向下更新到我们所有查询操作的最小粒度即可，而不用完全对整个线段树进行更新，是不是就完成了复杂度的优化！

这就是 $$O(logN)$$ 级别的批量更新思路，沿着这个思路我们继续来看 Push Down 操作。

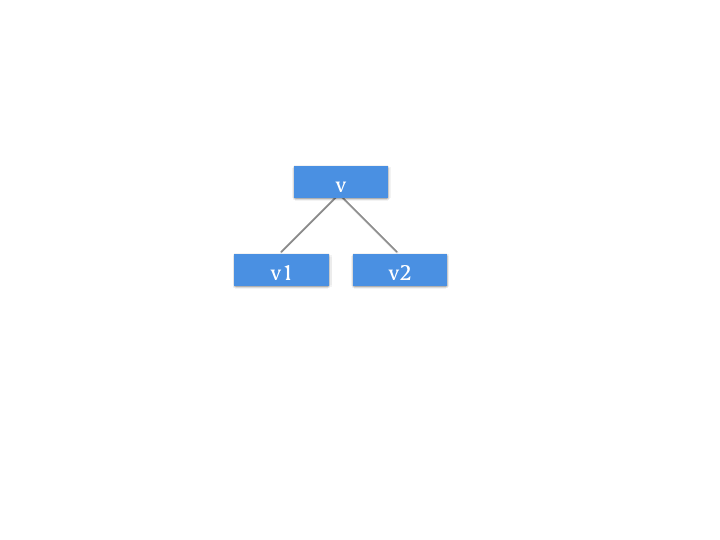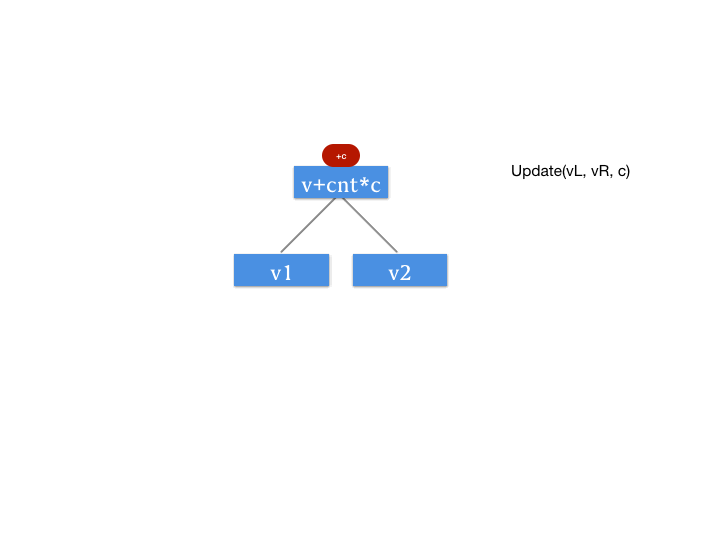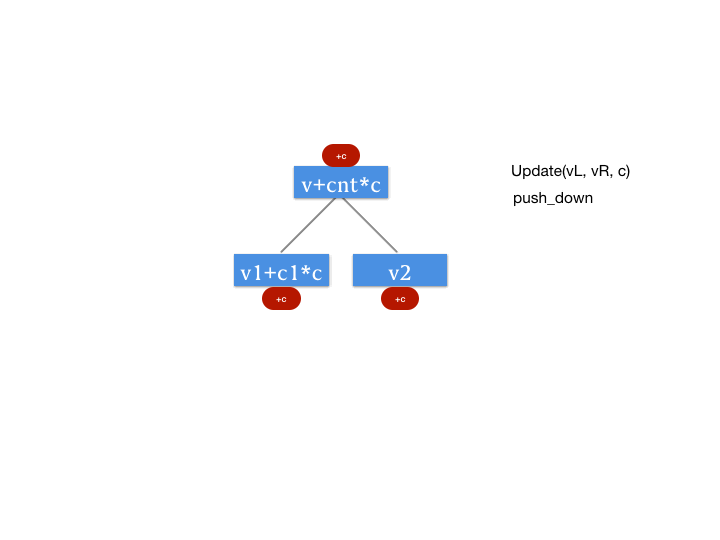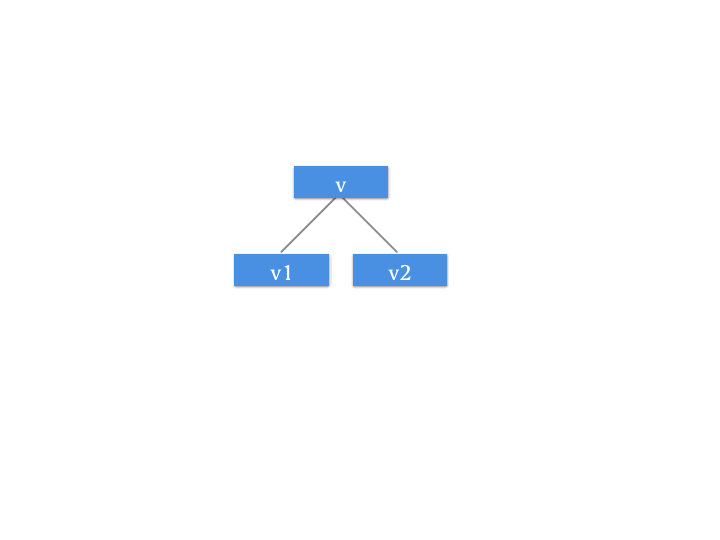
Push Down 操作

所谓 Push Down 操作，与我们第一篇文中所讲述的 Push Up 操作相反，Push Down 也就是向下更新的意思。因为我们要引入这个增量的记录数组，所以我们需要 Push Down 操作。

void push_down(int rt, int m) {
    // 如果增量数组有值，则我们将其向下更新
    // 此时的增量数组已经被放置在了最小颗粒度查询节点
    // 向下更新是为了更新到 sum 数组
    if (add[rt]) {
        // 先向下传递更新
        add[rt << 1] += add[rt];
        add[rt << 1 | 1] += add[rt];
        // 由于描述的是一个区间的批量更新，则这个区间要增加 detal * cnt 
        sum[rt << 1] += add[rt] * (m - (m >> 1));
        sum[rt << 1 | 1] += add[rt] * (m >> 1);
        // 传递后清空增量数组的父节点
        add[rt] = 0;
    }
}

Push Down 操作

在 Push Down 操作中，我们已经保证了这个更新是最小的可查询的粒度。那么，如果我们在后面要在后面去查询更细的粒度，我们要怎么办呢？其实，思路很简单，当我们查询的时候，也执行 Push Down 按照之前需要更新的范围继续向下更新，是不是就可以了。

我们来修改一下查询操作的代码，让他支持区间批量修改操作引入后的边查询、边修改的升级版。

int query(int L, int R, int l, int r, int rt) {
    if (L <= l && r <= R) {
        return sum[rt];
    }
    // 如果查询的时候遇到了增量数组，则向下更新一下
    // 因为后续要对下层区间和进行查询，所以需要最新的状态
    push_down(rt , r - l + 1);
    int m = (l + r) >> 1;
    int ret = 0;
    if (L <= m) ret += query(L , R , l, m, rt * 2);
    if (m < R) ret += query(L , R , m + 1, r, rt * 2 + 1);
    return ret;
}

同样的，由于 Update 区间操作也需要想查询一样最小的可更新粒度，所以我们在每查询到一个节点时，也对其增加一个 Push Down 操作，如此可以保证下方节点都是最新的更新态。

void update(int L, int R, int c, int l, int r, int rt) {
    if (L <= l && r <= R) {
        add[rt] += c;
        sum[rt] += c * (r - l + 1);
        return;
    }
    // 如果 update 更细粒度的节点，我们将其增量向下推一层获得最新状态
    push_down(rt, r - l + 1);
    int m = (l + r) >> 1;
    if (L <= m) {
        update(L, R, c, l, m, rt << 1);
    }
    if (m < R) {
        update(L, R, c, m + 1, r, rt << 1 | 1);
    }
    push_up(rt);
}

Unit Test

使用上面图示中的线段树，我们来写一个单元测试。分别对应以下操作：

建立区间和线段树；
查询 [1, 1] 节点；
查询 [1, 6] 节点；
更新 [1, 6] 节点，全部增加 4；
查询 [1, 6] 节点；
查询 [1, 2] 节点；

#include <iostream>
#include <vector>
using namespace std;

const int maxn = 100000;

vector<int> desc = {0, 1, 8, 3, 4, 7, 1, 6, 2};
int cur = 1;
int add[maxn << 2];
int sum[maxn << 2];

void push_up(int rt) {
    sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
}

void push_down(int rt, int m) {
    if (add[rt]) {
        add[rt << 1] += add[rt];
        add[rt << 1 | 1] += add[rt];
        sum[rt << 1] += add[rt] * (m - (m >> 1));
        sum[rt << 1 | 1] += add[rt] * (m >> 1);
        add[rt] = 0;
    }
}

void build(int l, int r, int rt) {
    add[rt] = 0;
    if (l == r) {
        cout << rt << " " << desc[cur] << endl;
        sum[rt] = desc[cur ++];
        return;
    }
    int m = (l + r) >> 1;
    build(l, m, rt * 2);
    build(m + 1, r, rt * 2 + 1);
    push_up(rt);
}

void update(int L, int R, int c, int l, int r, int rt) {
    if (L <= l && r <= R) {
        add[rt] += c;
        sum[rt] += c * (r - l + 1);
        return;
    }
    push_down(rt, r - l + 1);
    int m = (l + r) >> 1;
    if (L <= m) {
        update(L, R, c, l, m, rt << 1);
    }
    if (m < R) {
        update(L, R, c, m + 1, r, rt << 1 | 1);
    }
    push_up(rt);
}

int query(int L, int R, int l, int r, int rt) {
    if (L <= l && r <= R) {
        return sum[rt];
    }
    push_down(rt , r - l + 1);
    int m = (l + r) >> 1;
    int ret = 0;
    if (L <= m) ret += query(L , R , l, m, rt * 2);
    if (m < R) ret += query(L , R , m + 1, r, rt * 2 + 1);
    return ret;
}

int main() {
    build(1, 8, 1); // [1, 8, 3, 4, 7, 1, 6, 2]
    cout << query(1, 1, 1, 8, 1) << endl; // 1
    cout << query(1, 6, 1, 8, 1) << endl; // 1 + 8 + 3 + 4 + 7 + 1= 24
    update(1, 6, 4, 1, 8, 1); // [5, 12, 7, 8, 11, 5, 6, 2]
    cout << query(1, 6, 1, 8, 1) << endl; // 5 + 12 + 7 + 8 + 11 + 5 = 48
    cout << query(1, 2, 1, 8, 1) << endl; // 5 + 12 = 17
    return 0;
}

也许在读完之后，你会觉得这是一种很巧妙的区间增减操作，因为它是面向查询的。是的，这就是算法中的“惰性”（Lazy）思想，我们前面在并查集中也见到了这种优化。

本作品采用 知识署名-非商业性使用-禁止演绎（BY-NC-ND） 4.0 国际许可协议 进行许可。