用线段树再看 RMQ 问题

[28:30] 磊子:国内某特别爱招聘的大厂问过这么一道题:一个数组,要求得任意一个区间段内最大的数是多少。如果大家了解的话,就知道这题其实在考线段树….
其实 RMQ (Range Minimum/Maximum Query) 问题(又称区间最值问题)之前的文章中也有讲述,在 《RMQ 问题》 小节中,通过 ST 的二倍增 + 动态规划的思路,以 \(O(nlogn)\) 预处理以及查询 \(O(1)\) 复杂度下解决了这个问题。
也许你会想,在数组中直接遍历一下不就完了了吗,为什么要费这么多事情来做?直接遍历查找一遍也就是 \(O(n)\) 的复杂度?是的,其实背景是这样,因为我们需要做 \(K\) 次查询,这个 \(K\) 的上限很大,你可以理解成这个背景是在海量查询之下。
所以我们的出发点是通过一种优质的数据结构,将查询复杂度降低成 \(O(logn)\) 或者 \(O(1)\) 。由于查询次数是强需求,不是算法层面上可以优化的,所以在查询上的效率是我们主要解决的问题。
为了解决查询问题,这一篇文章我们引入 线段树(Binary Indexed Tree) 来优化 RMQ 问题的查询操作复杂度。
线段树的概念
我们如何理解线段树的定义呢?我们先抛开 RMQ 场景,先引入一个区间求和问题。
题目:给你一个数组 \(A\) ,它有 \(K\) 次查询,每次查询都给你 \(a\) 和 \(b\) 两个值,且 \(a < b < len(A)\) ,每次查询输出一个结果,代表 \(A[a] + A[a + 1] + ... + A[b]\) 的和。
简单描述一下就是给你数组中的两个下标,让你求出这一个区段的和是多少。
这次不用思考,我直接给出线段树是如何表示的:
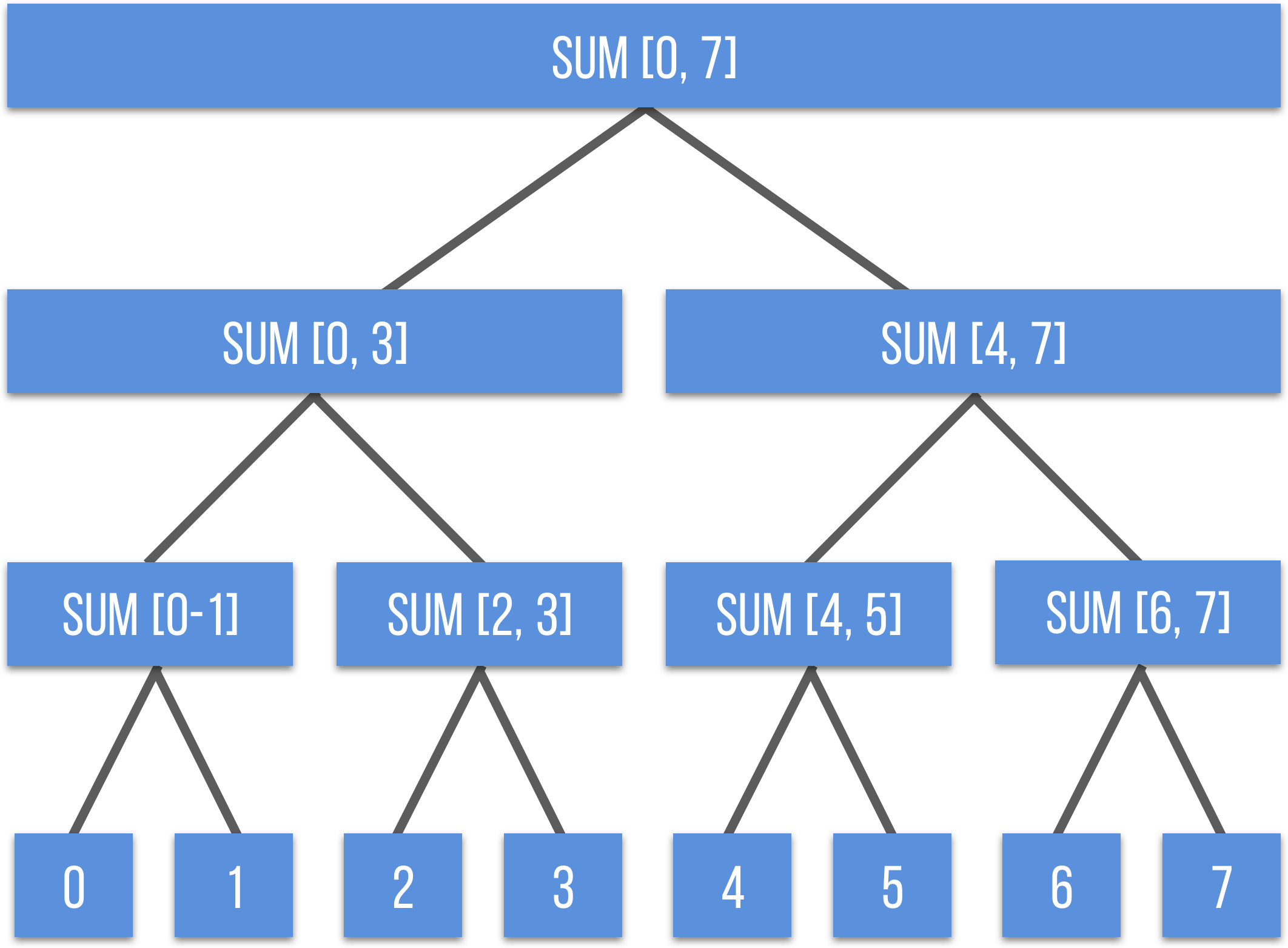
我们将整个数组区段, 通过二分区段的方式,将每一个区段的答案记录在二叉树每一个节点上。 当查询的时候只需要在这个二叉树中对边界做判断,然后拆分成子区间即可。
所以你应该可以理解,为什么它要叫“线段树”了吧,答案就是它会将整个区段抽象成一个大“线段”,然后根据表示的范围,二分划分成子“线段”。
如此我们给出线段树的定义: 线段树是一棵二叉树,线段树上每个结点对应的是序列的一段区间,每一个叶子结点对应的是序列的一个元素。树上的每个节点都维护一个区间,根维护的是整个区间,每个节点维护的是父亲的区间二等分后的其中一个子区间。 当有 \(a\) 个元素时,对区间的操作可以在 \(O(logn)\) 复杂度时间内完成。另外,从二叉树结构上,可以看出线段树是一棵完美二叉树(Perfect Binary Tree),即所有叶子的深度都相同,并且每个节点要么是叶子,要么有 2 个子树。
不同场景下线段树的功能
根据节点维护的数据含义不同,线段树可以提供不同的功能来满足各种各样的区间场景。下面我们先以上例中讲述的区间和为例,进而引出 RMQ 的使用场景。
求区间和
基础数据结构描述
任何数据结构都要从它的构造开始说起。以往我们想当然的认为,树状结构都应该以链式数据来存储。但其实二叉树使用数组描述可能更加简单明了。由于线段树也是二叉树,所以以下所有的表示方式我都使用数组来描述。
另外,假设我们的节点是 \(N\) 个,根据线段树结构的性质,我们会把这 \(N\) 个点当做叶子节点来看待。由于线段树是一棵满二叉树,假设它有 \(H\) 层,第 \(H\) 层节点数是 \(2^{H - 1}\) 个,一共 \( 2^H - 1\) 个节点。假设共 \(S\) 个节点,我们来推导一下:
\[ S = 2^H-1=2^{H-1}2-1=2N-1 \]那么只要让这个数组的大小开成节点数的两倍,就可以装满全部节点?其实是错误的! 我们先暂且记住,正确的答案应该是 \(4N\) ,具体原因可以查看下一篇《线段树实战要点》的 空间退化问题。
所以将线段树使用以下方式来声明。
const int maxn = 1e4 + 7;
int tree[maxn << 2];
一个知识基础:使用数组 tree[N] 来描述二叉树,对于节点 tree[i] ,它的左右孩子节点分别是 tree[2 * i] 和 tree[2 * i + 1]。在代码中为了稍微稍微做一些加速,所以我用 tree[i << 2] 和 tree[i << 2 | 1] 来表示。
Build 及 Push Up 操作
我们需要构造(Build)一棵线段树,与之同时我们还要考虑这棵线段树的 Push Up 操作。这个 Push Up 操作可以理解成是一种向上更新的概念。
void push_up(int rt) {
tree[rt] = tree[rt << 1] + tree[rt << 1 | 1];
}
通过代码可以看出,其实我们是使用下方的两个孩子节点,来更新其共同的父亲结点。从二叉树的角度来看,这个操作由于是向上方来更新维护的数据,所以我们称之为 Push Up 操作 。
具体的 Push Up 操作是为了实现什么效果呢?看这张动图你就懂了:
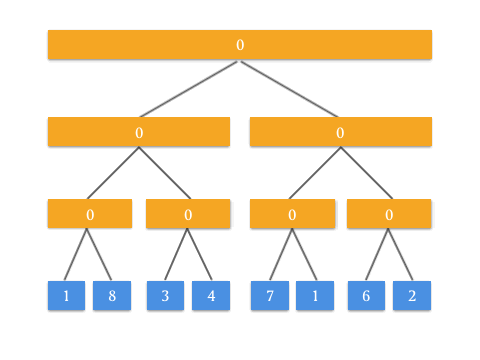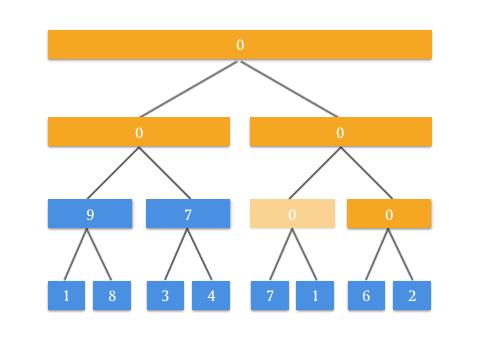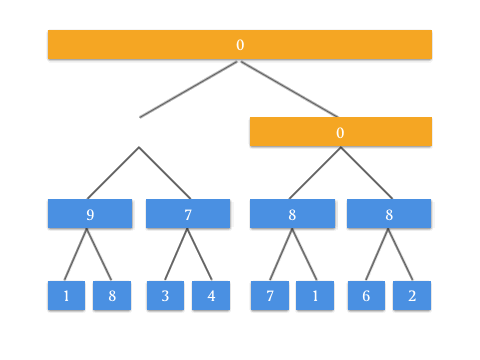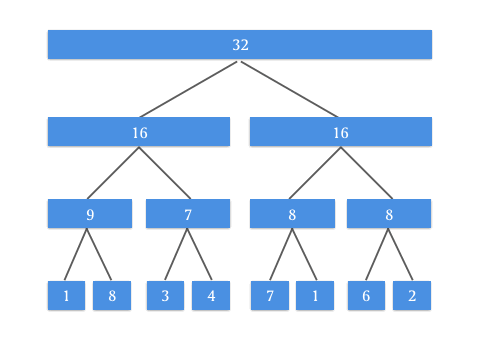
有了 Push Up 操作后,我们就可以自底向上来构建这棵二叉树了。由于我们知道根节点是 tree[1] ,而所有需要 Push Up 操作的元素都是最底部的叶子结点,所以在构造的时候需要先访问到最底部,递归调用 Push Up 向上更新即可。
/***
*
* @param l 当前节点描述范围的左边界
* @param r 当前节点描述范围的右边界
* @param rt 代表下标,tree[rt] 代表当前节点
*/
void build(int l, int r, int rt) {
if (l == r) {
tree[rt] = num[cur ++];
return ;
}
int m = (l + r) >> 1;
build(l, m, rt << 1);
build(m + 1, r, rt << 1 | 1);
// 这里递归到叶子执行一次向上更新
// 保证每一层都在上一层有数值之后执行
push_up(rt);
}
从这里可以看的出,其实我们构造一棵线段树,就需要执行多达 \(O(nlogn)\) 的复杂度。但是考虑到是海量查询的场景,而构造是一次性的(因为线段树是支持更新操作的,这个在本公众号后续篇幅将会讲到),所以从特殊场景下来看这个优化,是很合理的。
如此,我们完成了一棵线段树的创建。
瓜自己的归纳总结:线段树其实最重要的是“两操作,一思想”。两操作中,包括 Push Up 和 Push Down 两个操作,一个思想是 Lazy 延迟更新思想。Lazy 延迟更新其实在并查集中我们已经体会到了,在线段树中该如何使用了?这个需要等到线段树的区间更新操作才会讲到。Lazy 延迟更新和 Push Down 操作是紧密相连的。
Query 查询操作实现区间和
重头戏在这里,也是我们需要核心解决的问题 - 我们要如何做区间查询?
我们都知道,如果给你一个排序二叉树,当我查询是否有某个元素的时候,从根节点开始逐一比较节点大小,从而决策是向左走还是向右走就可以了。
而这里要面对的是一个线段树,线段树每一个节点代表的是一个区间。自然而然,我们只要弄清楚当前结点表示的是哪个区间,从而比较查询区间的边界值,就可以知道在下一层要往哪里走了。
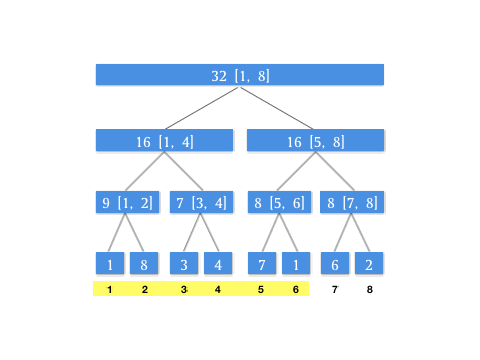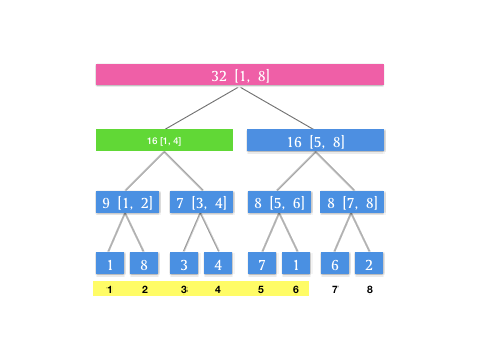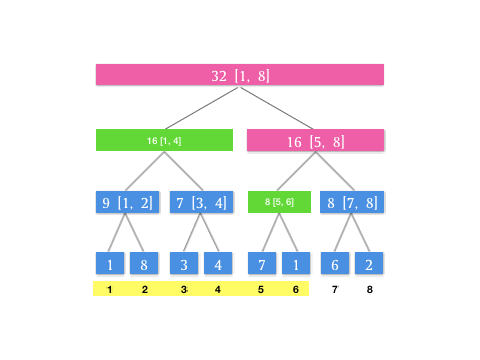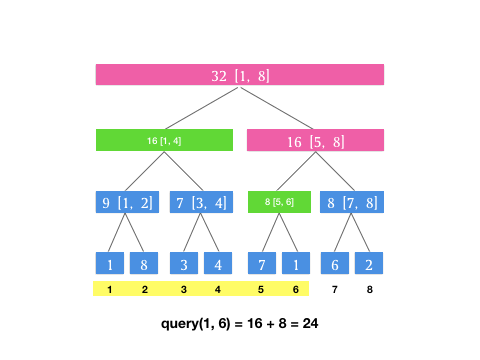
那如果遇到卡区间的情况怎么办?就是,如果我查询 \([1, 6]\) 这个区间,而当前结点是根节点 \([1, 8]\) ,左区间是 \([1, 4]\) 右区间是 \([5, 8]\) 这种情况,没有一个恰好能满足我们查询区域的区间范围。这时候我们只要把 \([1, 8]\) 划分成 \([1, 4]\) 和 \([5, 6]\) 分头查找就可以了。我们用树的遍历思想,其实就是两次递归可以了。
/***
*
* @param L 待查询区间左边界
* @param R 待查询区间右边界
* @param l 当前节点描述范围的左边界
* @param r 当前节点描述范围的右边界
* @param rt 代表下标,tree[rt] 代表当前节点
*/
int query(int L, int R, int l, int r, int rt) {
if (L <= l && r <= R) {
return tree[rt];
}
int m = (l + r) >> 1;
int ret = 0;
if (L <= m) ret += query(L, R, l, m, rt << 1);
if (R > m) ret += query(L, R, m + 1, r, rt << 1 | 1);
return ret;
}
单点更新操作
线段树的优势还在于我们可以对某一个节点做更新操作。这一点是 ST 算法不具备的能力。其实单点更新操作与 build 方法的想法十分雷同,我们只要递归到叶子节点,将更新值修改掉,之后逐渐向上执行 push_up 更新,其实就完成了新状态的维护。
/***
*
* @param p 待更新的下标,指的在 num 中的下标
* @param replace 待替换的值
* @param l 当前节点描述范围的左边界
* @param r 当前节点描述范围的右边界
* @param rt 代表下标,tree[rt] 代表当前节点
*/
void update(int p, int replace, int l, int r, int rt) {
if (l == r) {
tree[rt] = replace;
return ;
}
int m = (l + r) >> 1;
if (p <= m) update(p, replace, l, m, rt << 1);
else update(p, replace, m + 1, r, rt << 1 | 1);
push_up(rt);
}
单元测试
我们将以上的代码整合一下,自己模拟做有个单元测试。来验证这个支持单点修改的区间和查询场景。
#include <iostream>
#include <vector>
using namespace std;
const int maxn = 1e4 + 7;
vector<int> num(maxn);
int cur = 0;
int tree[maxn << 2];
void push_up(int rt) {
tree[rt] = tree[rt << 1] + tree[rt << 1 | 1];
}
/***
*
* @param l 当前节点描述范围的左边界
* @param r 当前节点描述范围的右边界
* @param rt 代表下标,tree[rt] 代表当前节点
*/
void build(int l, int r, int rt) {
if (l == r) {
tree[rt] = num[cur ++];
return ;
}
int m = (l + r) >> 1;
build(l, m, rt << 1);
build(m + 1, r, rt << 1 | 1);
push_up(rt);
}
/***
*
* @param L 待查询区间左边界
* @param R 待查询区间右边界
* @param l 当前节点描述范围的左边界
* @param r 当前节点描述范围的右边界
* @param rt 代表下标,tree[rt] 代表当前节点
*/
int query(int L, int R, int l, int r, int rt) {
if (L <= l && r <= R) {
return tree[rt];
}
int m = (l + r) >> 1;
int ret = 0;
if (L <= m) ret += query(L, R, l, m, rt << 1);
if (R > m) ret += query(L, R, m + 1, r, rt << 1 | 1);
return ret;
}
/***
*
* @param p 待更新的下标,指的在 num 中的下标
* @param replace 待替换的值
* @param l 当前节点描述范围的左边界
* @param r 当前节点描述范围的右边界
* @param rt 代表下标,tree[rt] 代表当前节点
*/
void update(int p, int replace, int l, int r, int rt) {
if (l == r) {
tree[rt] = replace;
return ;
}
int m = (l + r) >> 1;
if (p <= m) update(p, replace, l, m, rt << 1);
else update(p, replace, m + 1, r, rt << 1 | 1);
push_up(rt);
}
int main() {
// [1, 8, 3, 4, 7, 1, 6, 2]
num = vector<int>({1, 8, 3, 4, 7, 1, 6, 2});
int n = num.size();
build(1, n, 1);
cout << query(1, 3, 1, n, 1) << endl; // 1 + 8 + 3 = 12
cout << query(3, 8, 1, n, 1) << endl; // 3 + 4 + 7 + 1 + 6 + 2 = 23
update(3, 10, 1, n, 1); // [1, 8, 10, 4, 7, 1, 6, 2]
cout << query(1, 3, 1, n, 1) << endl; // 1 + 8 + 10 = 19
}
/*
* 输出
* 12
* 23
* 19
*
*/
完成测试,全部符合预期结果。😁
RMQ 问题
我们再来看 RMQ 问题。上面我们通过 Push Up 方法中,父节点等于两个孩子结点之和来构造的区间和树。通过这个思路来想,如果我们修改 Push Up 操作,将父亲节点等于两个孩子节点的最大值,是不是就完成了区间最大线段树?
void push_up(int rt) {
tree[rt] = max(tree[rt << 1], tree[rt << 1 | 1]);
}
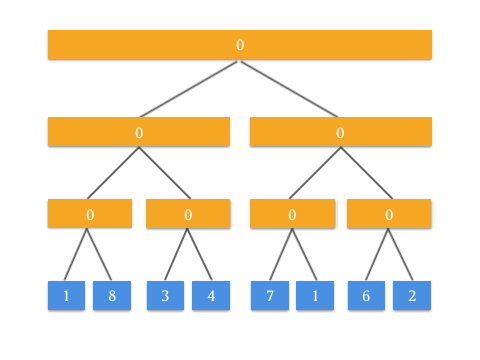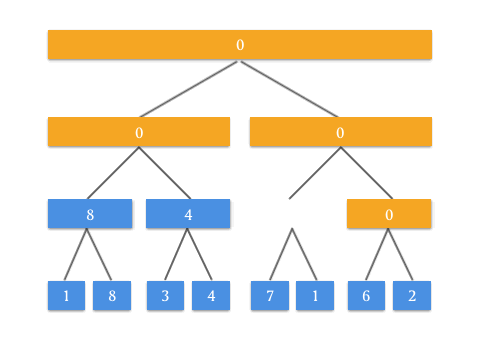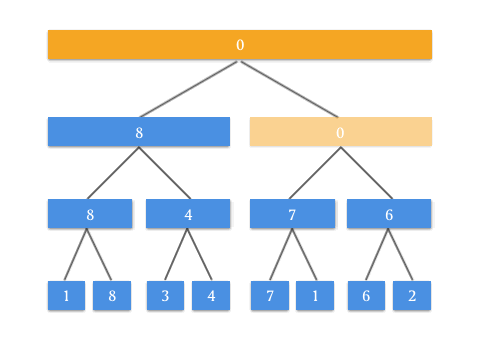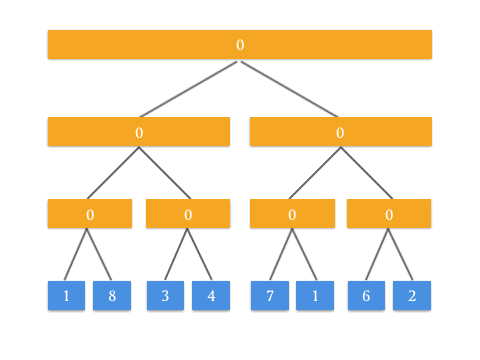
通过动画来表示,看起来很有道理!要实现 RMQ 问题的查询操作 query ,可能还要使用类似的思路做修改。这个修改就交给聪明的你了!也算是这篇文章给你出的一道思考题。
Push Up 操作的理解
为什么在线段树中 Push Up 操作如此重要?push-up 在英文中是俯卧撑的意思,由于线段树的叶子节点是对应我们实际数组中的每个元素,根据叶子节点,我们才能向上计算父亲节点的数值,通过子结点“撑起”父节点,意在于此。另外,由于线段树最关键的地方就在于父亲节点和孩子节点之间的关系是什么(其实有规律的二叉树都是这样),而 Push Up 操作却恰恰是用来描述这个关系的,所以 Push Up 是线段树最重要的操作之一。
线段树只所以区别于其他二叉树,原因是在于描述区间。二叉树往往是通过父亲来确定下一个孩子的位置(例如排序二叉树,插入节点向下填充),而线段树是通过孩子节点来确定父节点。从宏观上看,通常二叉树是向下更新,而线段树是向上更新。Push Up 是决定向上更新的策略是如何的,其重要性不言而喻了。
复杂度分析
无论是区间求和,还是 RMQ,通过线段树的数据结构来描述数据,实现了构造 \(O(4n)\) ,查询 \(O(klogn)\) ( \(k\) 代表可能出现的跨区域多路径),单点更新 \(O(logn)\) 。对比与我们用数组来描述原始数据,构造 \(O(N)\) ,查询 \(O(N)\) ,更新 \(O(1)\) 来说,在多查询的场景下,会有很大幅度的优化。
总结
通过 RMQ 线段树通过区间和线段树的简单转换,其实我们已经知道了,线段树能解决的问题不仅仅是这两个场景。其实只要是区间查询、区间操作问题中,并且区间内有确定运算结果场景下,都可以通过线段树来优化查询、更新的复杂度,例如:区间求 GCD(最大公约数)、区间求异或结果等等。
另外,对于线段树的探究远不止于此。后续还会有向下更新、区间更新这两个操作的加入,才能更大的发挥线段树的威力。这些都会在后续的文章中逐一分析!

本作品采用 知识署名-非商业性使用-禁止演绎 (BY-NC-ND) 4.0 国际许可协议 进行许可。