线段树实战要点

在上一公众号中《用线段树再看 RMQ 问题》，通过区间和的问题场景，已经学习了线段树的基本结构，以及其单点更新和区间查询的操作。但是在解《LeetCode-307 区域和检索 - 数组可修改》这道题目的时候，并不是一帆风顺的。所以这一篇文章我们来讨论一下线段树在做题时会遇到的一些坑。

空间退化问题

在《LeetCode-307 区域和检索 - 数组可修改》中，我们会遇到下标索引超出范围的 9/10 的 case。这也就是我们遇到的第一个最直观的坑。

刷题遇到的坑

上文我们说过，线段树是一棵 完美二叉树(Perfect Binary Tree)，可是题目中给出的结点个数不一定是 $$2^N$$ 次幂个。所以，这就带来了 空间结构退化的问题。

这里我们假设 N = 13 这个情况，然后我们通过之前的线段树代码进行代码实现后其结构变成了这样：

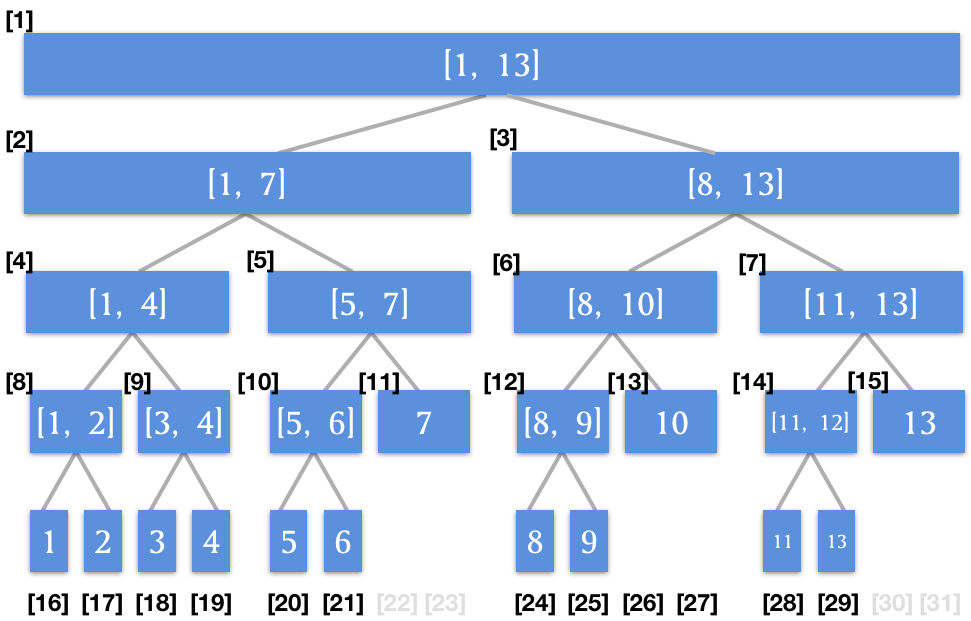
退化后的空间结构

通过上图，我们发现如果我们使用 2N = 26 的数组空间，实际上线段树已经覆盖了下标 31 ，这个场景下我们开 2N 的数组是不够的。

这里直接说结论：我们对线段树的描述数组开 4N 的空间，是绝对够用的。 具体的证明后续文章中单独写。

在谈 RMQ 问题

在第一篇文章中，我们讲了区间和的场景，将最重要的向上更新操作 Push Up 也做了介绍，并且给大家留了一道思考题：如何使用线段树来实现 RMQ 问题。

其实我们只需要修改两个地方：

在向上更新的时候，重新制定规则 - 父结点是两个子节点的大值；
在查询的时候，将结果取递归搜索的大值；

代码如下：

// 吸取上面的教训，现在我们数组开 4 倍
int tree[maxn << 2];

void push_up(int rt) {
    // 父结点是子节点中的最大值
    tree[rt] = max(tree[rt << 1], tree[rt << 1 | 1]);
}

int query(int L, int R, int l, int r, int rt) {
    if (L <= l && r <= R) {
        return tree[rt];
    }
    int m = (l + r) >> 1;
    int ret = 0;
    // 修改成递归查找区间最大值当做查询结果
    if (L <= m) ret = max(ret, query(L, R, l, m, rt << 1));
    if (R > m)  ret = max(ret, query(L, R, m + 1, r, rt << 1 | 1));
    return ret;
}

其实 RMQ 线段树并没有对线段树结构有任何改变，仅仅是修改了父子结点间的运算规则。

这样我们对于线段树的理解又加深了一层，因为“线段”并不仅仅代表着一段的加和，延伸来看，其实对某一块区间有着一定结果的运算规则，就可以使用线段树结构来优化查询和更新效率。

求解逆序数

这是一个很典型的统计场景，具体的题目是《LeetCode-493 翻转对》，其实就是在大学时《线性代数》课程中的求逆序数。由于在课程题目中，每个数都是有规律的，所以我们根据通项公式或者递推公式就可以求解。但是这道题目是给我们一个任意的数组，不存在数列所具有的特殊性，所以我们只能通过统计的效率来解决这个问题。

逆序数的简单介绍：假设我们有这样一组数 [2, 4, 3, 5, 1]，它有 5 个逆序对，分别是 (2, 1)、(4, 3)、(4, 1)、(3, 1)、(5, 1)，我们要求的答案是，以每个数为首位逆序数的个数，例如上述这组需要输出 [1, 2, 1, 1, 0]。

这种题我们应该如何考虑呢？我们换一个角度考虑，假设我们有一个以正整数范围的空线段树，仍旧是区间和线段树，这棵树的每一个叶子结点记录的是当前下标数字出现的次数。

我们需要的操作仍旧是 单点更新 和 区间查询。顺着以下思路来考虑问题：

构建一个 [1, MAXN] 范围的线段树，所有结点全部填 0。MAXN 代表数组中数字的最大值；
反向遍历传入的数组；
遍历到 x 的时候，对线段树做一次 query(1, x - 1) 操作，来记录有多少个比 x 小的数已经出现；
对线段树执行一次 update(x, num + 1) 操作，让线段树更新 x 的计数，做加 1 操作；
重复 3-4 操作，每次的 query 结果就是最后数组中对应的每一个值。

如上面的动画所示，Nums 的箭头代表遍历情况，Result 数组代表最终的返回结果，右边的操作记录是对线段树的操作 Log。

离散化

在上面求解逆序对的题目中，其求解的情况是不完整的。因为我们将数组中的数字全部映射到了数组的下标中，但是数组中的每个数字的取值范围是 $[-2^{31}, 2^{31}]$ ，如果出现负数和零那就无法完成映射了（因为线段树的下标都是正数）。在这种情况下我们要如何解决这个问题呢？

这里给出这两点思考方向：

虽然每个数字的取值范围是 $[-2^{31}, 2^{31}]$ ，但是给定数组的长度不会超过 50000；
逆序对只是比较了两个数的大小关系，而不用在意具体的数字是多少；

这两点是不是可以理解成，如果我们将这 N 个数，根据大小关系，映射到 [1, 50000] 这个范围内就可以解决问题了？

例如我们有这么一组数 [-1, -5, 0, 12, 8]，我们先升序排序处理一下 [-5, -1, 0, 8, 12] ，然后做一个 Hash 来映射到整数范围 {-5: 1, -1: 2, 0: 3, 8: 4, 12: 5}。通过 Hash 我们的数组变成了 [2, 1, 3, 5, 4] 。如此我们就可以继续使用上面的思路来求解了。

是不是这个思路非常巧妙~ 其实这种区间问题只涉及到大小关系的时候，都可以通过这个方法进行数字映射，从而投影到我们可求解的区域内。这种思路就叫做离散化。所谓的离散化官方的定义就是：把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。当我们对这类题目求解的时候，由于我们缩小了求解范围，从而算法的时间常数和空间复杂度都会有所降低，所以离散化也是最容易想到的优化点之一。

希望大家学习了逆序场景以及离散化的优化思路，可以自行 AC 这道题。另外，《LeetCode-493 翻转对》这个题目也可以通过这两个思路来尝试解决一下。

优美的 `notonlysuccess` 写法

notonlysuccess 是一个 ACM-ICPC 的前辈（网络号 id），因为他的线段树代码十分清晰且优雅，所以他的代码经常作为各个参赛选手的模板代码（虽然线段树最后大家都能徒手写出来）。具体何为优雅，下面放上 notonlysuccess 的线段数区间和的代码（其实在我公众号上，所有的代码风格都是在模仿 notonlysuccess，Respect ！！）：

#include <cstdio>

// 优雅点 1：参数宏定义
#define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1

const int maxn = 55555;
int sum[maxn << 2];

// 优雅点 2：PushUp 抽离
void PushUP(int rt) {
    sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
}

void build(int l, int r, int rt) {
    if (l == r) {
        scanf("%d", &sum[rt]);
        return ;
    }
    // 优雅点 3：能用位运算就用位运算
    int m = (l + r) >> 1;
    build(lson);
    build(rson);
    PushUP(rt);
}

void update(int p, int add, int l, int r, int rt) {
    if (l == r) {
        sum[rt] += add;
        return ;
    }
    int m = (l + r) >> 1;
    if (p <= m) 
        update(p , add , lson);
    else 
        update(p , add , rson);
    PushUP(rt);
}

int query(int L, int R, int l, int r, int rt) {
    if (L <= l && r <= R) {
        return sum[rt];
    }
    int m = (l + r) >> 1;
    int ret = 0;
    if (L <= m) ret += query(L , R , lson);
    if (R > m)  ret += query(L , R , rson);
    return ret;
}

总结

这篇文章讲述了在题目实战中使用线段树的一些技巧。包括：

数组上限大小；
RMQ 线段树实现方式；
逆序数使用线段树的求解思路；
离散化的优化方法；
notonlysuccess 版优雅线段树模板；

附录：关于线段树开 4N 空间的证明

先给出一条待证明的定理：当 $n \geq 3$ ，一个 $$[1, n]$$ 的线段树可以将 $$[1, n]$$ 的任意区间 $$[L, R]$$ 分解成不超过 $2\lfloor log_2{(n-1)} \rfloor$ 个子区间。

证明

用数学归纳法，证明上面的定理：

首先, $$n=3,4,5$$ 时，用穷举法不难证明定理成立。

假设对于 $$n= 3,4,5,...,k-1$$ 上式都成立，下面来证明对于 $n=k (k\geq 6)$ 成立：

分为 4 种情况来证明：

情况一

$$[L, R]$$ 包含根节点 $$(L=1, R=n)$$ ，此时， $$[L, R]$$ 被分解成为了一个节点，定理成立。

情况二

$$[L, R]$$ 包含根节点的左子节点，此时 $$[L, R]$$ 一定不包含根的右子节点（因为如果包含，就可以合并左右子节点，用根节点替代，此时就是情况一）。这时，以右节点为根的这个树的元素个数为 $\lfloor \frac{k}{2} \rfloor \geq 3$

$$[L, R] $$ 分成的子区间由两部分组成：

根的左子节点，区间数为 1
以根的右子节点为根的树种，进行区间查询，这个可以递归使用本定理。

所以综上， $$[L, R] $$ 一共被分成了 $1 + 2\lfloor log_2{(\lfloor \frac{k}{2} \rfloor - 1) \rfloor}$ 个区间

情况三

同情况二对称，不一样的是，以根的左子节点为根的元素个数为 $\lfloor \frac{k + 1}{2} \rfloor \geq 3$ 。

$$[L, R] $$ 一共被划分成了 $1 + 2\lfloor log_2{(\lfloor \frac{k}{2} \rfloor - 1) \rfloor}$ 个区间。

从公式可以看出，情况二的区间小于等于情况三的区间数，于是只需要证明情况三的区间数符合条件就行。

\begin{aligned} & 1 + 2\lfloor log_2{(\lfloor \frac{k + 1}{2} \rfloor - 1) \rfloor} \\ = & 1 + 2\lfloor log_2{(\lfloor \frac{k + 1}{2} \rfloor) \rfloor} \\ \leq & 1 + 2\lfloor log_2{(\frac{k + 1}{2}) \rfloor} \\ = & 1 + 2\lfloor log_2{(k-1)-1} \rfloor \\ = & 2\lfloor log_2{(k-1)} \rfloor - 1 \\ < & 2\lfloor log_2{(k-1)} \rfloor \end{aligned}

所以，情况二和情况三定理成立。

情况四

$$[L, R]$$ 不包括根节点以及根节点的左右子节点。

于是，剩下的 $2\lfloor log_2{(k-1)} \rfloor$ 层，每层最多两个节点。

所以， $$[L, R]$$ 最多被分解成了 $2\lfloor log_2{(k-1)} \rfloor$ 个区间，定理成立。

综上

综上，当 $n \geq 3$ ，一个 $$[1, n]$$ 的线段树可以将 $$[1, n]$$ 的任意区间 $$[L, R]$$ 分解成不超过 $2\lfloor log_2{(n-1)} \rfloor$ 个子区间。

证毕。

但需要注意的是， $2\lfloor log_2{(n-1)} \rfloor$ 是上界，但不是最小上界。所以我们来测试一下 $4n \geq 2\lfloor log_2{(n-1)} \rfloor$ 是否成立？

\begin{aligned} 4n & \geq 2\lfloor log_2{(n-1)} \\ 2n & \geq log_2{(n-1)} \\ 4^{n} & \geq n - 1 \end{aligned}

所以我们发现，当 $$n$$ 取自然数 $$1, 2, 3, ...$$ 均成立。

本作品采用 知识署名-非商业性使用-禁止演绎（BY-NC-ND） 4.0 国际许可协议 进行许可。