RMQ（Range Maximum Query) 问题

今天的算法可能有点难，但是如果我们只需要会使用 RMQ 问题的 ST 算法模板，这种程度就已经可以了！因为 RMQ 问题除了最优解的 ST 算法，剩下的都是高级数据结构的应用，例如：线段树、树状数组、Splay、Treap 甚至是主席树（额，我什么都没有暗示，业界就是这个名字）。好了今天我们从两个角度来解决这个问题。ST 算法和线段树。当然如果你对高级数据结构感兴趣，我也会在以后的文章中更新这个系列。

注意，学 RMQ 问题与图论没有直接关系，而是 Tarjan 算法中其中的一个重要步骤之一。再次验证了高级算法都是由基础的问题排列组合而来！🧐

这篇文章我们只讲 RMQ 问题以及 RMQ 的最优解法 ST 算法。

引子

RMQ 的英文是 Range Maximum(Minimum) Query，翻译过来其实就是区间求最值的意思。问题描述：对于长度为 n 的数列 A，回答若干询问 $$RMQ(A, i, j)(i, j <= n)$$ ，返回数列A中下标在 [i, j] 里的最小(大）值。

在这个问题中，我们需要关注的是查询操作，查询可能是海量的，所以如果我们对数据进行快速的预处理，然后在外面处理后的数据结构中进行快速查询，其实就是最理想的状态。

另外，注意是“在给定的区间内”，那么则说明区间在后续的查询时没有变化。所以我们可以理解成在区间确定后，我们其实已经拿到了所有查询情况的答案！对于这种对给定范围内求值的算法，我们对其归类为离线算法。（当然对应的还有在线算法，后面讲 Tarjan 算法时我们再详谈）

我们先来尝试下暴力：

nums = [3, 2, 4, 5, 6, 8, 1, 2, 9, 7]

def query(l, r):
    res = nums[0]
    for i in range(l, r + 1):
        res = max(res, nums[i])
    return res

我们发现每一次查询都是一个 $$O(n)$$ 的操作，在海量的查询面前，效率就十分低下了。或许你觉得 $$O(n)$$ 还能接受？但是人总是喜新厌旧、择优选择的 🙄 。

ST 算法解决 RMQ 问题

ST 算法的全名是 Sparse Table Algorithm，中文一般管 Sparse Table 称作稀疏表。原理是基于二进制的倍增、动态规划思想的。笔者感觉还是有一定难度的。

大概描述一下 ST 算法的两个步骤：

1. 预处理

ST 算法原理上还是动态规划，我们用 $$a(1...n) $$ 表示待查询的一组数，设 $$f(i, j)$$ 表示从 $$a(i)$$ 到 $$a(i + 2^j - 1) $$ 这个范围内的最大值。也就是说 $$a[i]$$ 为起点，连续 $$2^j$$ 个数的最大值。由于元素个数为 $$2^j$$ 个，所以从中间平均分成两部分，每一部分元素个数刚好为 $2^{j - 1}$ 个，也就是说，把 $$f(i, j)$$ 划分成 $$f(i, j - 1)$$ 和 $f(i + 2^{j - 1}, j - 1)$ 。

我画个图来描述一下这个场景：

区间描述

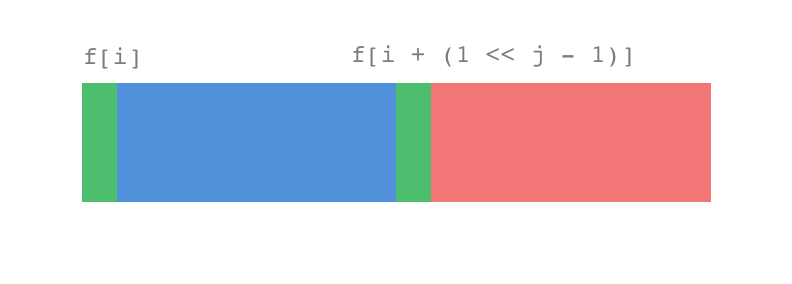
整个区间的最大值一定是左右两部分最大值的较大值，满足动态规划的最优化原理（子状态影响父状态）。很显而易见的状态转移方程：

f(i,j)=max(f(i,j-1),f(i+2^{j-1},j-1)

边界条件是：

\[ f(i, 0)=a(i) \]

这样我们就可以在 $$O(nlogn)$$ 的复杂度内预处理 f 结果数组。

我们举一个例子，还用上面暴力求职的数据：[3, 2, 4, 5, 6, 8, 1, 2, 9, 7] ， $$f(1, 0)$$ 表示第 1 个数起，长度为 $$2^0 = 1$$ 的最大值，其实就是 3。

同理

$\[f(1, 1) = max(3, 2) = 3\]$ $\[f(1, 2) = max(3, 2, 4, 5) = 5\]$ $\[f(1, 3) = max(3, 2, 4, 5, 6, 8, 1, 2) = 8\]$

规律就是 2 倍增区间。代码实现一下~

nums = [3, 2, 4, 5, 6, 8, 1, 2, 9, 7]

f = [[0 for _ in range(1, 40)] for _ in range(1, 31)]


def rmq_initial():
    n = len(nums)
    for i, num in enumerate(nums):
        f[i][0] = num
    for j in range(1, 31):
        for i in range(0, n):
            if i + (1 << (j - 1)) >= n:
                break
            f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1])

查看一下预处理之后的 $$f$$ 查询数组：

[3, 3, 5, 8, 8, 0]
[2, 4, 6, 9, 9, 0]
[4, 5, 8, 9, 0, 0]
[5, 6, 8, 9, 0, 0]
[6, 8, 8, 8, 0, 0]
[8, 8, 9, 9, 0, 0]
[1, 2, 9, 0, 0, 0]
[2, 9, 9, 0, 0, 0]
[9, 9, 0, 0, 0, 0]
[7, 0, 0, 0, 0, 0]

这是一个什么东西呢，我们先行（其实是 f 数组的第二个下标）来看：

\left\{\begin{matrix} 3&3&5&8&8 \end{matrix}\right\}\tag{1}

由于我们确定了第一个下标为 0，则这行的含义就是：

\left\{\begin{matrix} max(3)&max(3, 2)&max(3, 2, 4, 5)&max(3, 2, 4, 5, 7, 8, 1, 2)&max(3, ..., 7) \end{matrix}\right\}

简单概括就是，对于 f[0][a] 来说，代表的就是 max(nums[0....0 + 2^a)。这是第二个下标的含义。对应的，对于 f[b][0] 来说，代表的就是 max(nums[b - 2 ^ b + 1 ... b]) 。好好理解这个数组含义，后面的查询操作就显而易见了。

2. 查询操作

我们继续思考区间最大值问题，假设我要查询 [l, r] 这个区间，那么我们如果找到两个子区间，他们的并集精确覆盖到 [l, r] 是不是就满足要求了？

ST 由于使用2倍增，它的边界不好完美覆盖全部 case，所以我们在查询的时候需要简单的做交集操作来约束范围。在上面对于 f 数组的理解中，我们知道了 f 数组的横纵坐标分别代表首末的边界数值，我们的想法就是：为了满足所有区间均可求，我们使用两个范围，确定其最大值和最小值，只要能完全精准覆盖 [l, r]即可求得结果。这里我简单证明一下：

我们假设一个中间量 k ，并满足：

2^k\leq r-l+1\leq2^{k+1}\\ k\leq log_2{(r-l+1)}

然后我们考虑一下 l 开始的 $$2^k$$ 个数和以 r 结尾的 $$2^k$$ 个数 这个区间是否可以覆盖我们的 $$[l, r]$$ 区间。当且仅当：

k\geq log_2{(r-l+1)}-1

取极限，我们令 $$k = log(r - l + 1)$$ ，那么在 f 数组中只需要查询：max(f[l][k], f[r - (1 << k) + 1][k]) 就可以了，是不是很容易？🙄 （其实一点都不容易，但是一般教程都会这么写，我也就这么写，hhhhh）。

ST区间合并覆盖

def rmq_query(l, r):
    k = math.log(r - l + 1) / math.log(2)
    return max(f[l][k], f[r - (1 << k) + 1][k])

如此，我们就通过了 $$O(1)$$ 的方式完成了指定区间任意范围的 RMQ。对于海量数据查询的需求完成了最高度的优化。但是由于 ST 算法需要一个 2 倍增的预处理，所以整体的复杂度在 O(nlogn)。如此评估下来，其实如果查询量极少的情况下，我们用暴力法的时间开销 $$O(n)$$ 是优于 ST 算法的，但是 ST 是在大量查询的场景下，所以算法也和业务技术方案一样，有适合于业务的，也有不适合于业务的，一切从业务出发来解决问题就好啦~

我们掌握了以上方法，尝试着套着 ST 算法的模版，来 A 道题尝试一下，你会立马发现它的奇妙（能解决问题）！

ST 算法解决 RMQ 问题

我们来看一道 RMQ 的裸题：HDU-5443 The Water Problem

这种题目分两步走，拍上模板，然后写逻辑！HDU 不支持 Python，我们用 C++ 写一版就好啦~

#include <iostream>
#include <cstdio>
#include <math.h>
#define maxn 1000000 + 4

using namespace std;

int f[maxn][20];

// 模板
void rmq_initial(int n) {
    for (int j = 1; j < 21; ++ j) {
        for (int i = 0; i < n; ++ i) {
            if (i + (1 << (j - 1)) >= n) break;
            f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
        }
    }
}

// 模板
int rmq_query(int l, int r) {
    int k = log(r - l + 1) / log(2);
    return max(f[l][k], f[r - (1 << k) + 1][k]);
}

int main() {
    int T, n;
    cin >> T;
    while (T --) {
        scanf("%d", &n);
        for (int i = 0; i < n; ++ i) {
            scanf("%d", &f[i][0]);
        }
        rmq_initial(n);
        int l, r, q;
        scanf("%d", &q);
        while (q --) {
            scanf("%d%d", &l, &r);
            printf("%d\n", rmq_query(l - 1, r - 1));
        }
    }
    return 0;
}

HDU-5442-AC-STATE

结尾

RMQ 问题其实还有很多解发，笔者比较常用的就是 ST 算法和线段树。但是 ST 算法无论从空间复杂度、时间复杂度还是代码量上来看，都优于线段树，但是 ST 算法往往只局限在 RMQ 问题，而具有区间操作的线段树的变化更加灵活，并且是在线查询，可以支持数据源的变化。所以在业务场景下，多变性和业务健壮性的工程角度来看，线段树是一个更加不错的选择。下一篇文章我们来讨论如何利用线段树来解决 RMQ 的问题。

本作品采用 知识署名-非商业性使用-禁止演绎（BY-NC-ND） 4.0 国际许可协议 进行许可。