在之前的两篇文章中，我们讲述了「最大流问题」和「Ford-Fulkerson 最大流求解方法」，当然在阅读这篇文章之前，我需要你有以上两篇文章的基础，请在阅读上面两篇文章后再来进行阅读。这篇文章我们来讲述一个二分图匹配问题。并且将这个问题转化为最大流问题模型来解决。

为了引出二分图匹配问题，我们首先给出一个实际问题的例子：

计算机 CPU 指派问题

在我的 N 核计算机上有 K 个任务。每个任务在工作时都得霸占 CPU 一个完整的核心，并且每个 CPU 核心不是所有任务都能处理，只能处理其中几种任务。我们的问题是在一次处理过程中，最多能够处理的任务数是多少？

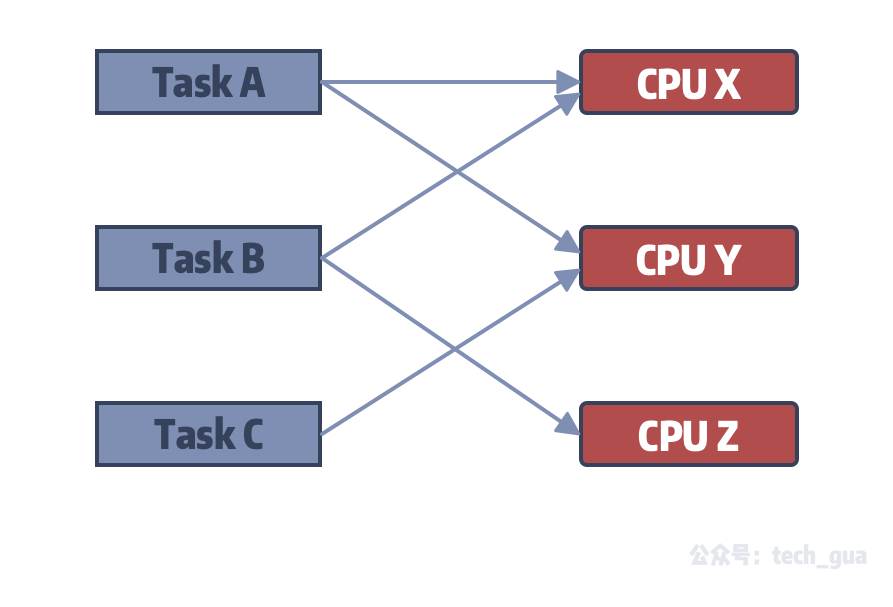
上图中我描述了一组样例，在这组样例中 Task A 只能有 CPU X 和 CPU Y 来处理，Task B 只能由 CPU X 和 CPU Z 来处理，而 Task C 只能有 CPU Y 来处理。

问题抽象与二分图最大匹配

其实上面对于样例的描述我们已经可以画出一个有向图了。我们将 Task 和 CPU 都转换成图节点：

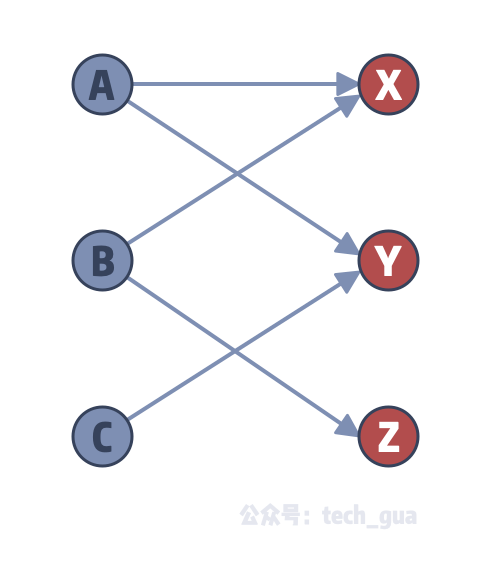
我们发现，这个图他可以分成左右两部分，并且左边这些节点相互之间没有相连的边，同样的右边节点也没有相连的边，所有的边都是左右两个部分之间的连接，对于这种特点的图，在图论中有一个专有的名词，二分图。

而对于这个问题，我们需要求最多有多少个任务可以被处理，也就是说根据关系找到一种 Task 和 CPU 的配对方式，使得配对数量达到最大。这种二分图求最大匹配数量的问题，我们称之为二分图最大匹配问题。

思考和转化问题

使用结果反向启发

我们可以考虑一种上方样例中的最大匹配方案，如下图所示就是一种情况：

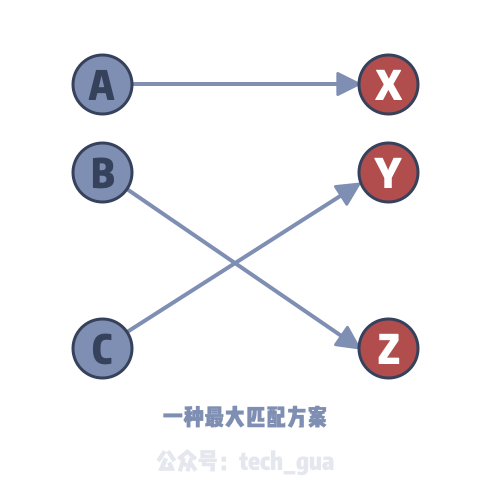
我们观察一下上面的答案，其实是删除了 A → Y 和 B → X 这两条边。有没有感觉这种删除边的操作我们之前也处理过呢？这里我们从最终的结果出发来启发你的思维，如果你没有发现什么玄机，我们再来做一个新的变化。

赋权值量化图

第二种变化，我们对于原图的任意一条边增加权值为 1 。

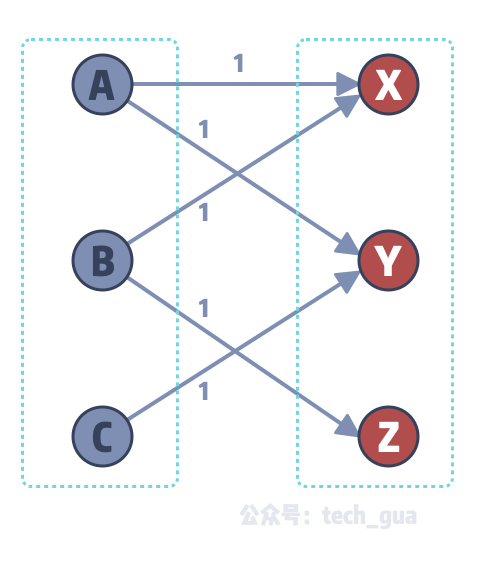
变化之后，我们只看左右两个部分，此时思考问题的角度就变成了从左边的节点集合到右边节点集合 最多可以保留几条边？换句话说，也就是从左到右流入的最大权值是多少？当然不是任意一条边都能保留，因为每一节点只能有一个出度和一个入度，这个条件也就确保了我们求得的结果是匹配数。

既然我们需要保证左边集合中，每一个节点有且只有一个出度，而右边的节点有且只有一个入度，那么我们不妨将这个题目再次进行转换，我们将边权值定义为流量容量，且节点也增加权值，且定义为当前节点的流量值。

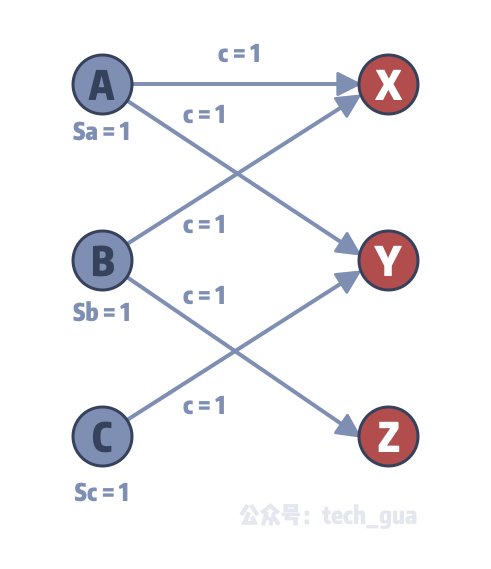
此时，我们将问题 变成了一个多限制流量源点（A、B、C）多汇点（X、Y、Z）的最大流问题 ！但是我们并不会求多限制源点多汇点的最大流，因为我们没有学过具体的方法。但是我们发现，这些源点流量是被限制的，可不可以通过一个方法让这些点自然带上这些限制的流量？当然有，加一条有容量的边！

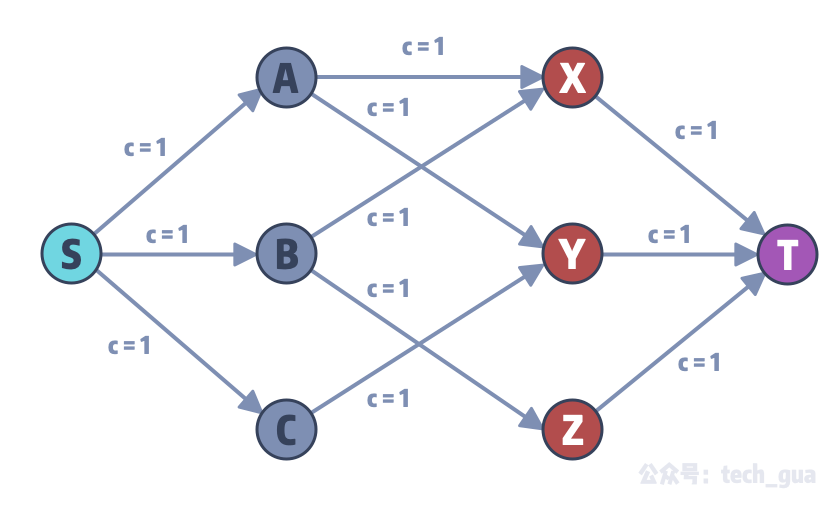
我们在图的两边分别增加了一个超级源 S 和超级汇 T 两个点，其中 S 具有无穷流量。然后分别增加了 S 到 A、B、C 的边，X、Y、Z 到 T 的边，且这些边的容量都是 1。通过容量我们限制了 A 、B、C 的流量都是 1，并且由于都是以一个单位统计，则流入 T 的流量结果就是最大的匹配数 。

此时这个问题已经转化成了之前介绍的 最大流问题 。是不是十分神奇呢~

FF 最大流解决二分图最大匹配问题

经过了一系列花活，我们将二分图最大匹配问题，又转换成了之前的网络流的最大流问题。此时我们掏出之前学习过的 Ford-Fulkerson 最大流求解方法来实现以下即可：

#include <iostream>
#include <string>
#include <vector>
using namespace std;

const int MAX_V = 1e4 + 5;

struct Edge {
    // 终点、容量、反向边
    int to, cap, rev;
    Edge(int _to, int _cap, int _rev): to(_to), cap(_cap), rev(_rev) {}
};

vector<Edge> G[MAX_V];
bool used[MAX_V];

void add_edge(int from, int to, int cap) {
    G[from].push_back(Edge(to, cap, G[to].size()));
    G[to].push_back(Edge(from, 0, G[from].size() - 1));
}

/**
*
* @param c 当前节点
* @param t 汇点
* @param f 当前路径中的容量最小值
* @return
*/
int dfs(int c, int t, int f) {
    if (c == t) {
        return f;
    }
    used[c] = true;
    for (int i = 0; i < G[c].size(); ++ i) {
        Edge &e = G[c][i];
        if (!used[e.to] && e.cap > 0) {
            int d = dfs(e.to, t, min(f, e.cap));
            if (d > 0) {
                e.cap -= d;
                G[e.to][e.rev].cap += d;
                return d;
            }
        }
    }
    return 0;
}

int main() {
    // A, B, C 为节点 0, 1, 2
    // X, Y, Z 为节点 3, 4, 5
    // S, T 为节点 6, 7

    // 题目描述的 A, B, C 和 X, Y, Z 的关系
    add_edge(0, 3, 1);
    add_edge(0, 4, 1);
    add_edge(1, 3, 1);
    add_edge(1, 5, 1);
    add_edge(2, 4, 1);

    // 模拟超级源 S 点
    add_edge(6, 1, 1);
    add_edge(6, 2, 1);
    add_edge(6, 3, 1);

    // 模拟超级汇 T 点
    add_edge(3, 7, 1);
    add_edge(4, 7, 1);
    add_edge(5, 7, 1);

    // 求最大流
    int flow = 0;
    for (;;) {
        memset(used, 0, sizeof(used));
        int f = dfs(6, 7, 1);
        if (f == 0) {
            cout << flow << endl; // 3 验证通过
            return 0;
        }
        flow += f;
    }
}

总结

网络流的神奇之处就在于，我们可以将其他类型的题目通过图抽象、加点权约束，从而转换成网络流中的经典问题。这篇将 二分图最大匹配 转换成 最大流问题 的思维过程，想必会让你对图算法又了新的认识。算法题目的考察从广义上来讲，就是在考察你 是否能将这个问题对应到一个你熟悉的求解模型和方法上 ，如果你抽象得当，你就可以利用已有的算法，去高效的求解这个问题。

“万物皆可网络流”，真正有趣的才刚刚开始！