在上一节《初识最大流问题》中，已经讲到了网络流中的一个经典问题 - 最大流问题。同上一篇的方式一样，这篇文章你要带着以下两个问题来阅读：

• 怎样搜索到一条增广路？
• 如何利用搜索到的增广路求解最大流问题？
• Ford-Fulkerson 算法求最大流的原理是什么？

如何求得最大流

我们继续引用上文的例子：

假设有这么一个例子，这次 2019-nCoV 疫情让口罩变成了稀缺资源。所以，全国各地都在为武汉捐献物资。假设现在因为种种原因，我们只能通过地面线路来运输口罩物资，并且每一条线路是有流量限制的。假设不考虑运输速度，并且源点 S （杭州）的口罩物资产量是足够多的，我们需要求解汇点 T（武汉）在不计速度的情况下能收到多少物资？

首先我们拍脑袋来自己探索一个算法，计算最大流。

我们的目标是找到增广路，所以我们制定一个策略：通过 DFS 深度优先搜索，来检索一条增光路，然后计算从 S 到 T 的最大流量，并在所有的边流量容量中将其扣除。反复按照这种操作，来迭代我们每次扣除之后的残余网络，最后无法再找到增广路则停止搜索，求得我们的“最大流”。

我们来做一个动图来描述一下这个过程：

这个动图中描述的算法包括以下三步：

1. 搜索出一条增广路；
2. 在这条路径中所有的边容量减去这条增广路的流量，如果容量为 0 则拆边；
3. 返回操作一，如果没有增广路则得到答案。

在这道例题中，我负责任的告诉你，答案确实是最大流 23。但是求解的过程是错的！ 为什么会造成过程是错的，但是答案是对的的情况？原因是因为这个流网络的最大流刚好是我们这种做法所得到的答案。那正确的解法应该是怎样的？我们在来看一个图：

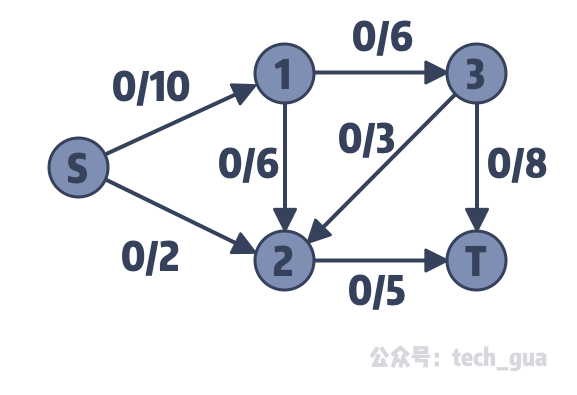
我们按照上文的方法来求解一下最大流。

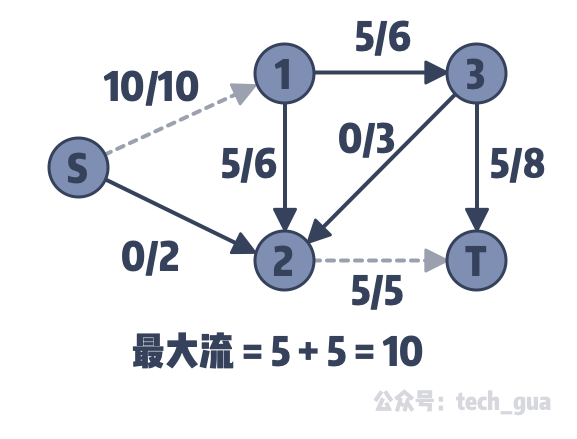
我们通过上述的三步流程进行演算，最终获得的残余网络如上，求得最大流是 10。

但是我在这里再次负责的告诉你，这个结果是不正确的！理由如下：

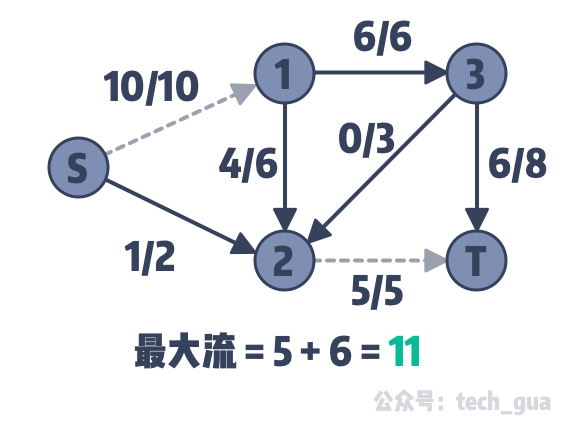
按照这种方式来处理流量，可以获得最大流 11 的答案，这是更优的结果。由此我们证明了上述我们自己构造的算法是有问题的。可是问题出在哪呢？我们对比一下两张图的流量差：

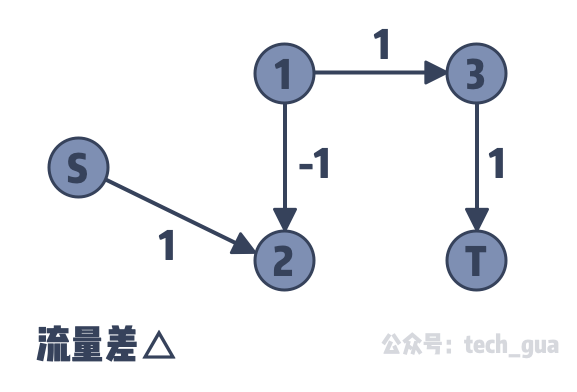
通过对比流量差，我们 发现其中 1 → 2 会通过将流量推回这种操作，从而得到新的流 。为什么要这么做呢？其实原因就是 因为对一条增广路不一定输入这条增广路的上限流量就能保证全局的最大流量 。再提高一个维度来看我们之前的思路，其实一直是“贪心”思想在引导我们加流和拆边操作，但是贪心并不能获得全局最大流量，这也是之前动态规划能够解决贪心对于全局最优解无法实现的问题 。

既然我们无法得知如何取得全局最优解，有一种思路就是，继续增加可能情况。具体怎么加，其实只要对上面错误算法增加一个操作就可以：在第 2 步中，在边权减去流量之后，并对这条边再做一条反向边，并且容量变成对应消耗流量的相反数 。接着用图来解释：

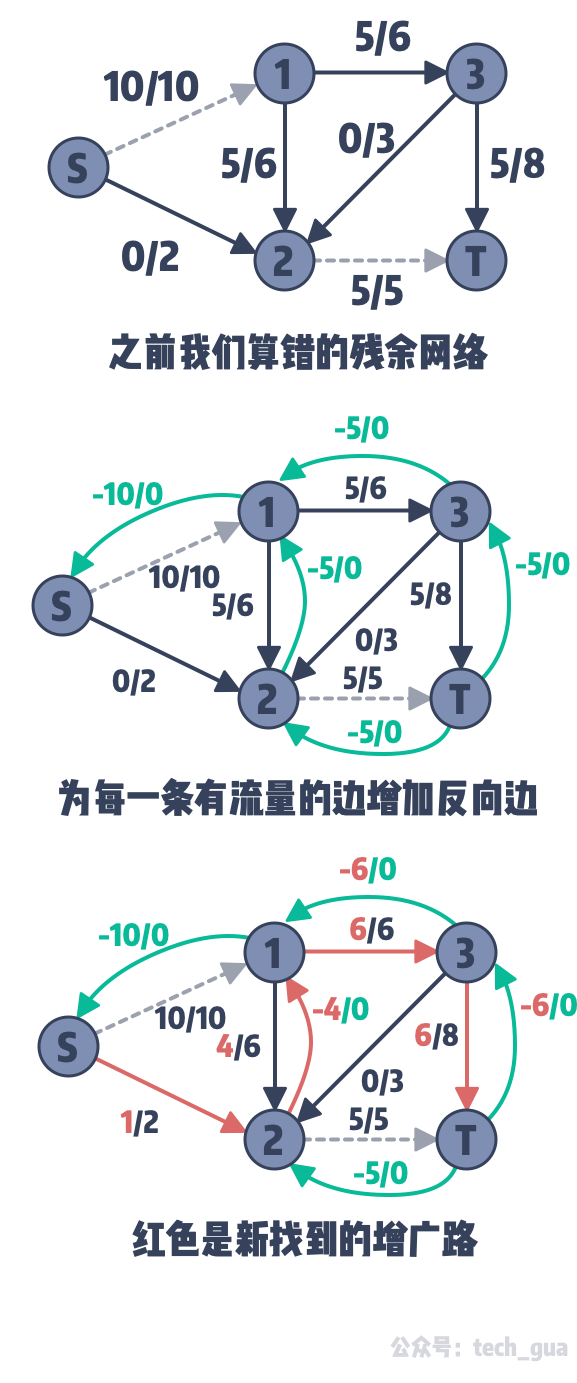
通过上述操作，我们又多找出了一条增广路（即图中红色的那条路），并且为 T 多增加了 1 个单位的流量，如此求得了最后的答案是 11。

可能你会问，为什么这种做法是合理的，可以求得最终的结果呢？其实就涉及到我们上一篇所讲的 「最大流最小割定理」，这个证明我后续会放到 PC 端小册上，因为它属于延伸知识。而对于不想看枯燥的证明过程的朋友来说，你只要想明白这件事就可以了，看下图：

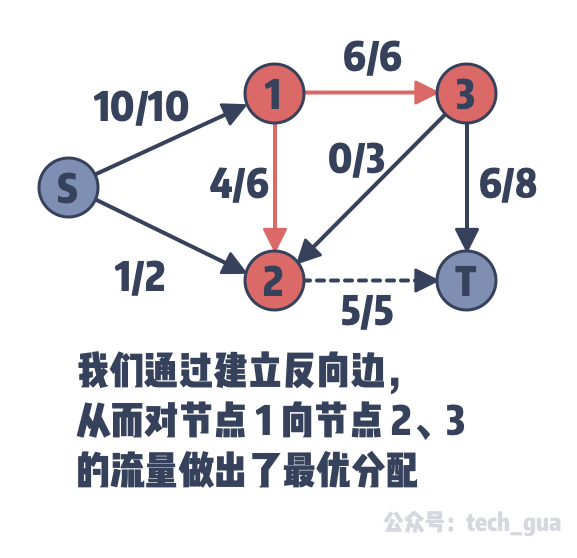
以上，我们知道了怎么去求得最短路，下面来总结一下梳理后的算法：

1. 搜索出一条增广路；
2. 在这条路径中所有的边容量减去这条增广路的流量，并建立流量为增广路增加流量相反数的反向边；
3. 返回操作一，如果没有增广路则得到答案。

这也就是本文标题中的 Ford-Fulkerson 最大流方法。

如何代码实现查找增广路？

在这篇文章中，我们均使用 DFS 深度优先搜索来寻找增广路。这里直接给出代码：

/**
  * 查找增广路
  * @param c 当前节点
  * @param t 汇点
  * @param f 当前路径中的容量最小值
  * @return
  */
int dfs(int c, int t, int f) {
    // 如果当前节点是汇点 t，直接返回容量最小值，即增广路增加的流量
    if (c == t) {
        return f;
    }
    // 记忆化搜索染色
    used[c] = true;
    // 遍历 c 节点下一个节点
    for (int i = 0; i < G[c].size(); ++ i) {
        Edge &e = G[c][i];
        // 如果这个节点未被访问到，并且其当前容量大于 0
        if (!used[e.to] && e.cap > 0) {
            // 访问到最深层节点
            int d = dfs(e.to, t, min(f, e.cap));
            if (d > 0) {
                // 当前边容器减少
                e.cap -= d;
                // 反向边容量增加
                G[e.to][e.rev].cap += d;
                return d;
            }
        }
    }
    return 0;
}

其实这段代码也就是 Ford-Fulkerson 最大流方法 的核心代码，剩下的就是一个 while(true) 的迭代，直到找不到增广路，查找停止，得到最大流我们的代码结束。

当我们理解了算法逻辑，代码实现起来也就异常的简单了！

复杂度分析

由于我们使用深度优先搜索的情况，所以我们可以假设如果有一个图，其中有一条增广路的中间某一条边的容量是 1，但其实最后结果是不走流量的，但是在 DFS 的过程中每次还会先算到它。在这种情况下，假设我们图的最大流是 F ，则在这张图上 Ford-Fulkerson 方法就进行了 F 次的深度优先搜索。每一次搜索都会去搜 E 条边，所以其时间复杂度是 O(F ·|E|)。

这里的最大流也许会非常大，所以使用 Ford-Fulkerson 方法会产生超级高的时间开销。所以你也明白了，后续的高效算法都是在查询增广路上做文章来优化 Ford-Fulkerson 方法。

一些边沿知识

在这篇文章中，我们 一直称作 Ford-Fulkerson 方法，而不是 Ford-Fulkerson 算法，其实是因为 Ford-Fulkerson 给出了最大流问题中的三个重要思想 - 增广路、残余网络、反向边 。依赖于 Ford-Fulkerson 方法，后续的最大流算法如 Edmond-Karp 算法 、Dinic 算法 将会在 Ford-Fulkerson 基础上优化时间复杂度。

另外提一句，Edmond-Karp 算法的作者 Manning Karp 因为在算法理论方面的巨大贡献，获得了 1985 年的图灵奖。

计算机理论科学家 Manning Karp

关于 Manning Karp，最著名的就是他的《Karp 的 21 个 NP 完全问题》，有兴趣可以看 Wikipedia 对于这篇论文的介绍

相对于解决问题的算法而言，其思想程度更加重要，所以它是一种方法！

Ford-Fulkerson 方法的 代码实现

#include <iostream>
#include <string>
#include <vector>
#include <regex>
using namespace std;

const int MAX_V = 1e4 + 5;

struct Edge {
    // 终点、容量、反向边
    int to, cap, rev;
    Edge(int _to, int _cap, int _rev): to(_to), cap(_cap), rev(_rev) {}
};

vector<Edge> G[MAX_V];
bool used[MAX_V];

void add_edge(int from, int to, int cap) {
    G[from].push_back(Edge(to, cap, G[to].size()));
    G[to].push_back(Edge(from, 0, G[from].size() - 1));
}

/**
  *
  * @param c 当前节点
  * @param t 汇点
  * @param f 当前路径中的容量最小值
  * @return
  */
int dfs(int c, int t, int f) {
    if (c == t) {
        return f;
    }
    used[c] = true;
    for (int i = 0; i < G[c].size(); ++ i) {
        Edge &e = G[c][i];
        if (!used[e.to] && e.cap > 0) {
            int d = dfs(e.to, t, min(f, e.cap));
            if (d > 0) {
                e.cap -= d;
                G[e.to][e.rev].cap += d;
                return d;
            }
        }
    }
    return 0;
}

int main() {
    // 本文开篇时给出的示例
    add_edge(0, 1, 16);
    add_edge(0, 3, 13);
    add_edge(1, 2, 12);
    add_edge(2, 3, 9);
    add_edge(2, 5, 20);
    add_edge(3, 1, 4);
    add_edge(3, 4, 14);
    add_edge(4, 2, 7);
    add_edge(4, 5, 4);

    int flow = 0;
    for (;;) {
        memset(used, 0, sizeof(used));
        int f = dfs(0, 5, 1000);
        if (f == 0) {
            cout << flow << endl; // 23 验证通过
            return 0;
        }
        flow += f;
    }
}

总结

相信看了本文，已经开始对网络流中最大流问题有了更深的认识。但是上述实现的复杂度我们并不能在做题当中接受，所以接下来，我们将继续探讨更加高效的最大流算法。