最近公众号群里逐一攻克图论的相关习题，其中有几道题就是关于拓扑排序的，所以我想到写这么一篇博客来链接一下算法和工程之间的关系。在这篇文章中，我认定你是有图论基础的，对于什么是图、节点、边已经有了简单的认识。

也许你会觉得图论对于我们很陌生，但其实它无处不在，只是我们业务中接触的太少了。

从 DAG 开始说起

DAG 是图论中常见的一种描述问题的结构，全称是有向无环图（Directed Acyclic Graph）。所谓的有向无环图也很好解释，边是有方向的、且图中没有环。下面我给一个 DAG 图的示例：

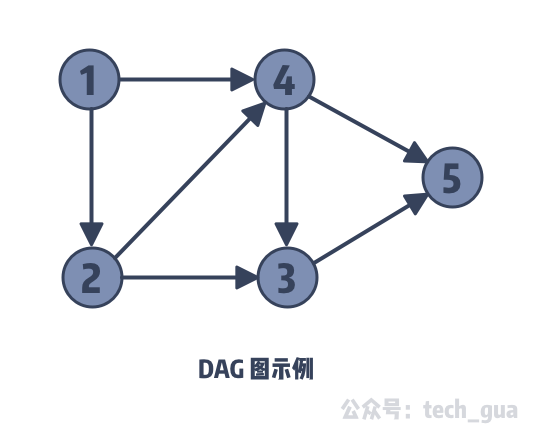
图中你可能会有一个疑问，DAG 不是没有环吗？可是图中有好几个环呀。在有向图中，环即回路。如果对于回路你比较陌生，可以查看我之前的一篇文章 - 欧拉回路。

零入度拆点与拓扑排序

除了 DAG ，我们还需要了解一个概念，就是在图中对于一个节点的入度和出度。这个概念其实很简单，在有向图中对于一个节点来说，如果一条边的终点是这个节点，这条边就是这个节点的入度；如果一条边的起点是这个节点，这条边就是这个节点的出度。

这些简单的概念了解之后，我们来说 拓扑排序（Topological Sorting）。

其实在笔者上大学的时候就有这么一个疑问，为啥这个排序方法要叫“拓扑排序”呢？我们可以如此来理解这个名字，因为图论是拓扑学中的一个很小的分支，拓扑学研究的问题往往关注点是在物体间的关系，而并非物体的形状和大小。

拓扑排序就是这样，我们根据一个图来描述的一系列关系，从而得到一个节点的排序方案，这就是今天要说的拓扑排序。拓扑排序是按照以下规律进行操作的：

1. 从图中找出一个入度为 0 的点，加入追加的维护的结果序列；
2. 对图进行拆点操作，拆掉这个点以及所有相连的边；
3. 反复执行 1 → 2 这个操作，直到结果数组中已经有整个图的结果序列；

通过一个动画来了解拓扑排序的过程：

简单了解完拓扑排序之后，可能你会有一个疑问：为什么要确保 AOV（Activity On Vertex Network）中一定要确保是一个 DAG？另外，对于一个 DAG，其拓扑排序是唯一的吗？

其实如果当一个有向图中存在回路，则在处理环的时候你就会发现没有入度为 0 的节点，则拓扑排序的算法无法进行下去。

对于一个 DAG，它的拓扑排序也不是唯一的，如果当前处理的一张图中，拥有多个入度为 0 的节点时，可以任意的对其中一个进行拆点。但为了简化问题的处理方式，我们往往是根据遍历顺序来进行拆点操作。

了解拓扑排序应用

很多读者都会关注：我学了这个东西有什么用？作为一个“运用场景客服”，我从刷题和工程两个角度来说明拓扑排序的广泛应用。

[LeetCode-207] 课程表

题目大意就是，有 [0, n - 1]这 n 门课程，我们已经知道这些课程的先修关系。例如：课程 1 需要先完成课程 2 才能学习。根据先修关系，判断这 n 门课程是否可以全部修完？示例 1:

输入: 2, [[1,0]]
输出: true
解释: 总共有 2 门课程。学习课程 1 之前，你需要完成课程 0。所以这是可能的。

示例 2:

输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0；并且学习课程 0 之前，你还应先完成课程 1。这是不可能的。

我们简单的来分析一下题目：其实这道题主要就是来找什么情况下，我们无法完成全部课程的场景。由于每个课程是有关系的，所以我们通过构建一个有向图来描述这个问题。如题目中给出的样例 1 ，我们如下建图即可。

那么什么时候我们无法完成全部课程呢？其实当建好图就已经明白了，如果这个有向图存在环，则无法完成全部课程。因为没有 0 入度的节点作为切入点来进行先修。在例 2 中我们也能发现最简单的例子：

可以看出，这是一种不可能完成的情况。因为两个课程构成了一个回路。所以转换一下思路，我们按照课程的先修关系建图，之后进行一次拓扑排序算法的操作，逐渐拆掉入度为零的节点。如果最终可以具有拓扑序，则课程可以全部全部完成。

如何存图

大学的时候所学习的《数据结构》课程我们学过，一张图可以通过两种方法：邻接表和邻接矩阵。邻接矩阵我们很好理解，就是一个二维数组，下标是节点编号，g[x][y] 代表 x 和 y 这两个节点是否有边。但是在这个问题中，我们仅需要每个节点的出度子节点，所以只要有一个出度节点集合就可表达。所以我们选用邻接表来实现这个问题。这时候没刷过题的同学会有一个惯性思维：不用数组那就用链表咯，用链表就要先做一个 Class（Struct），里面再做一个 next 的指针数组。内心 OS 就开始：这道题好难，图论太难了，我不会！其实并不是这样的。我们仅仅需要存每一个节点的后继节点，所以也可以通过二维数组来存。我们定义 g[x][] 代表节点 x 的后继节点数组，仅此就够了。另外，我们再建立一个 indegree 一维数组，来记录每个节点的入度信息。

class Solution {
public:
    #define maxn 10005
    vector<int> g[maxn];
    int indegree[maxn];

    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        // 建图操作
        for (auto& n : prerequisites) {
            g[n[1]].push_back(n[0]);
            // 每个节点的入度
            indegree[n[0]] ++;
        }

        queue<int> que;
        for (int i = 0; i < numCourses; ++ i) {
            // 搜索起点，将入度为 0 的点加入处理队列
            if (indegree[i] == 0) {
                que.push(i);
            }
        }

        while (!que.empty()) {
            int cur = que.front();
            que.pop();
            // 模拟拆点，计数减一
            numCourses -= 1;
            for (auto& n : g[cur]) {
                indegree[n] -= 1;
                // 发现入度为零，加入处理队列
                if (indegree[n] == 0) {
                    que.push(n);
                }
            }
        }
        // 检查是否所有点都被拆掉
        return (numCourses == 0);
    }
};

归纳

对这道题目来归纳一下整个构思的流程。首先我们知道了所有的课程有一个先修依赖关系，所以通过图来描述这种关系。再次我们了解如果当这个有向图有回路的时候，则无法完成全部课程，结果就应该输出 false ，如此就可以将这道题目抽象成拓扑排序问题。

Carthage 中的依赖校验算法

Carthage 是一个三方的开源的依赖管理工具，主要针对于 Apple 生态，兼容 iOS、macOS 等工程。在所有的依赖管理工具中，决议算法是将依赖打包进入工程的重要一环，例如 iOS 中另一个依赖管理工具 CocoaPods 中的 validate 阶段、前端使用的 Yarn Selective dependency resolutions 。这里我们只关注 Carthage ，因为它用 Swift 编写，其逻辑更容易读懂。另外 Carthage 也将算法逻辑完全解耦，其核心代码部分都在一个文件中。在 Carthage 的 Algorithm.swift 我们可以发现，作者已经在注释中对拓扑排序做了一定的介绍，其实就是本文上面篇幅所讲到的内容。

public func topologicalSort<Node: Comparable>(_ graph: [Node: Set<Node>]) -> [Node]? {
    // 找出所有入度为 0 的节点，也是后面的任务数组（复用）
    var sources = graph
        .filter { _, incomingEdges in incomingEdges.isEmpty }
        .map { node, _ in node }

    // 因为后面要进行删点操作，做一次 copy
    var workingGraph = graph
    // 第一轮删除所有入度为 0 的节点
    for node in sources {
        workingGraph.removeValue(forKey: node)
    }

    // 拓扑序结果数组
    var sorted: [Node] = []

    while !sources.isEmpty {
        sources.sort(by: >)
        // 取出一个入度为 0 的节点
        let lastSource = sources.removeLast()
        // 结果数组插入
        sorted.append(lastSource)
        // 遍历当前节点所有的入度节点
        for (node, var incomingEdges) in workingGraph where incomingEdges.contains(lastSource) {
            // 更新入度节点数组
            incomingEdges.remove(lastSource)
            // 更新图信息
            workingGraph[node] = incomingEdges

            // 如果当前入度为零
            if incomingEdges.isEmpty {
                // 加入处理数组
                sources.append(node)
                // 图拆点
                workingGraph.removeValue(forKey: node)
            }
        }
    }

    // 如果图中的节点都被拆掉，返回拓扑顺序
    return workingGraph.isEmpty ? sorted : nil
}

在 Carthage 中，这段代码是用来对依赖图做最终的校验环节的，具体的递送流程可以看这里。在其单元测试中，也有对应的拓扑排序的测试用例。我们用 AOV 网图绘制了一下提及的关系：

测试用例中最终结果是：

let sorted = topologicalSort(validGraph)
expect(sorted) == [
  "Argo",
  "PrettyColors",
  "Result",
  "Commandant",
  "ReactiveCocoa",
  "ReactiveTask",
  "Carthage",
]

我们发现最终就是一个拓扑序优先、字典序排列的一个结果。为什么在依赖版本处理中会有这样的校验方法呢？原因就是为了防止 引入仓库的循环依赖问题。拓扑排序通过拆点处理，确定了依赖图是一个 DAG 网图，从而验证了依赖关系的合理性。

拓扑排序仅仅是依赖处理的校验中的一环，为了 App 的编译、连接，对依赖的校验其实还有很多复杂的处理流程。在客户端工程中，也还有很多与算法切合的地方，等待我们一一挖掘，发现其精妙。